# Matplotlib compatibility patch for Pyodide
import matplotlib
if not hasattr(matplotlib.RcParams, "_get"):
    matplotlib.RcParams._get = dict.get

Matrixframe

Matrixframe is commerciële software waarmee constructies kunnen worden doorgerekend. MatrixFrame gebruikt symbolen die erg lijken op de symbolen gebruikt bij de opleiding in Delft. Voor studenten is er een gratis studentenlicentie (registratie bij MatrixFrame vereist) en een versie die alleen op het TU Delft netwerk (eventueel via VPN verbinding) werkt. Als je de studentenlicentie hebt aangevraagt maar niet ontvangen, kun je een ticket indienen via deze link.

Een aantal punten zijn van belang bij het gebruik van MatrixFrame:

• Bij het gebruik van matrixframe zal je altijd stijfheden van de elementen moeten invoeren (‘profielgegevens in MatrixFrame’). Dit heeft MatrixFrame nodig om de constructie door te rekenen, ook al is dat voor de krachtsgrootheden in statisch bepaalde constructies niet nodig. In het geval dat deze gegevens niet bekend zijn kan je een willekeurige grote waarde nemen onder ‘Handmatige invoer’ waarmee je een oneindige stijve staaf kan modelleren. Als de waarde een paar ordegroottes groter is dan de andere waardes is het al goed, bij een te grote waarde ontstaan er numerieke issues.

• Soms kunnen elementen overlappen zonder dat je het ziet.

Een uitgebreide handleiding met meer opties is hier te vinden. Daarnaast biedt de officiële documentatie ook meer uitleg.

Over het algemeen zijn de volgende stappen vereist:

Algorithm (Invoer en uitvoer constructie in MatrixFrame)

1. Maak een nieuw project - ‘2D-Raamwerk’ en klik ‘Ok’. De optie ‘1D-ligger’ en ‘2D-vakwerk’ zijn versimpelingen van de ‘2D-Raamwerk’-optie. De optie ‘3D-Raamwerk’ en ‘3D-Vakwerk’ kan je proberen, maar daar krijgt men over het algemeen hoofdpijn van.

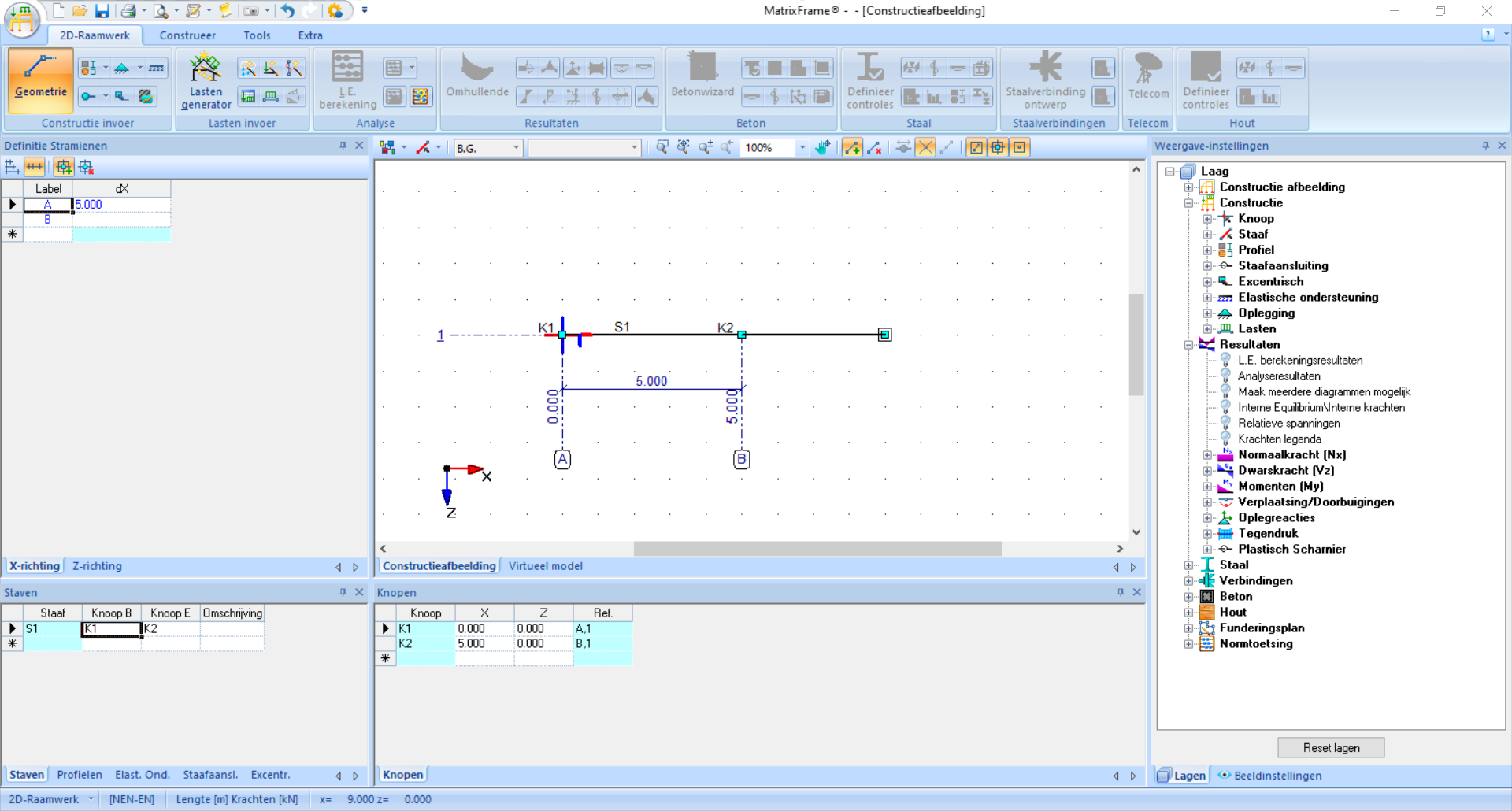
2. Je beland direct in de ‘Geometrie’ interface. Klik in het grid om je geometrie te vormen. De coördinaten zijn zijn zichtbaar in de onderbalk en de afmetingen verschijnen tijdens het klikken. Gebruik Esc op je toetsenbord om te stoppen of op een volgend element te beginnen die niet vastzit aan het uiteinde van het vorige element. Pas eventueel afmetingen aan met behulp van de stramienen aan de linkerkant of de coördinaten aan de onderkant van het scherm.

3. Ga verder met de ‘Profielgegevens’ interface. Ook als deze informatie niet bekend is is het invoeren hiervan vereist. Onder ‘Profielen’ - ‘Handmatige invoer’ kan je een \(A\), \(I\) en \(E\) invullen. Het is niet mogelijk een waarde van \(0\) of \(\infty\) in te vullen, daarvoor zal je een kleine of grote numerieke waarde moeten invoeren. Tip, \(\cdot10^6\) kan je invoeren als e6 Vergeet niet op ‘Pas toe op alles’ te klikken! Linksonder in het scherm zie je nu achter elke staaf een profielnaam staan.

4. De volgende stap is het toevoegen van opleggingen. Er zijn een aantal standaard opties, maar je kan ook handmatig translatie- en rotatierichtingen vastzetten. De opleggingen kan je plaatsen op de knopen of langs een staaf (in dat geval wordt er een nieuwe knoop gemaakt).

5. Nu kunnen we verder met scharnieren. In een raamwerk is standaard alles momentvast verbonden. Per staaf kan je voor elk uiteinde aangeven of dit een scharnier moet worden door op een deel van die staaf te klikken. Als twee aansluitende staven scharnierend zijn verbonden is het niet nodig om beide staafuiteindes scharnierend te maken, ééntje is genoeg.

6. De laatste configuratiestap is het toevoegen van belastingen. Je kan verschillende belastingsgevallen (B.G.) toevoegen, maar zolang je er maar één hoeft door te rekenen is het niet nodig die opties aan te passen. Voor elke belasting is het wel nodig de waarde en richting aan te geven en de staaf aan te klikken waarop deze last werkt. In het venster onderin het scherm kan je deze ook nog aanpassen.

7. Nu alles geconfigureerd is kan je op L.E. berekening (linear-elastische berekening) klikken. Er opent zich dan een dialoogvenster die foutmeldingen geeft als er iets niet klopt

8. Om de resultaten te bekijken zijn er een aantal opties. De oplegreacties kunnen los worden getoond. Let op, de richting van de pijlen geeft de daadwerkelijke richting aan van de krachten en koppels; een eventueel minteken geeft aan dat die kracht in de negatieve richting van het assenstelsel werkt.

9. De snedekrachtenlijnen kunnen ook worden getoond. Deze kunnen per snedekracht getoond worden volgens de vervormingstekens zoals we die gewend zijn. Mochten de vervormingstekens niet zichtbaar zijn kan je inzoomen of de schaal vergroten onder ‘Weergave-instellingen’ - ‘Beeldinstellingen’ - ‘Eigenschappen’ - ‘Resultaten’ - ‘Normaalkracht (Nx)’/’Dwarskracht (Vz)’/’Moment (My)’ - ‘Vorm’ - ‘Schaal’ - Voeg waarde in en klik op ‘Toepassen’. Als een staaf wordt aangeklikt zijn links in het scherm alle snedekrachten en verplaatsingen van die staaf zichtbaar. Onderin het scherm worden een aantal karakteristieke waardes getoond. De waardes worden getoond volgens het lokale assenstelsel.

10. Ook verplaatsingen kunnen worden getoond. Het aantal decimalen kan worden aangepast onder ‘Weergave-instellingen’ - ‘Beeldinstellingen’ - ‘Eigenschappen’ - ‘Resultaten’ - ‘Verplaatsingen/Doorbuigingen’ - ‘Label’ - ‘Decimalen’ - Voeg waarde in en klik op ‘Toepassen’.

11. Tot slot kunnen waardes op specifieke posities worden afgelezen met de spion functie. Klik daarvoor een staaf aan en voer onder ‘Invoer pos:’ een locatie in in het lokale assenstelsel. De tabel en grafische weergave toont dan waardes van snedekrachten en verplaatsingen op dat punt.

Als voorbeeld bepalen we de uitwendige statisch onbepaaldheid van deze constructie.

Example

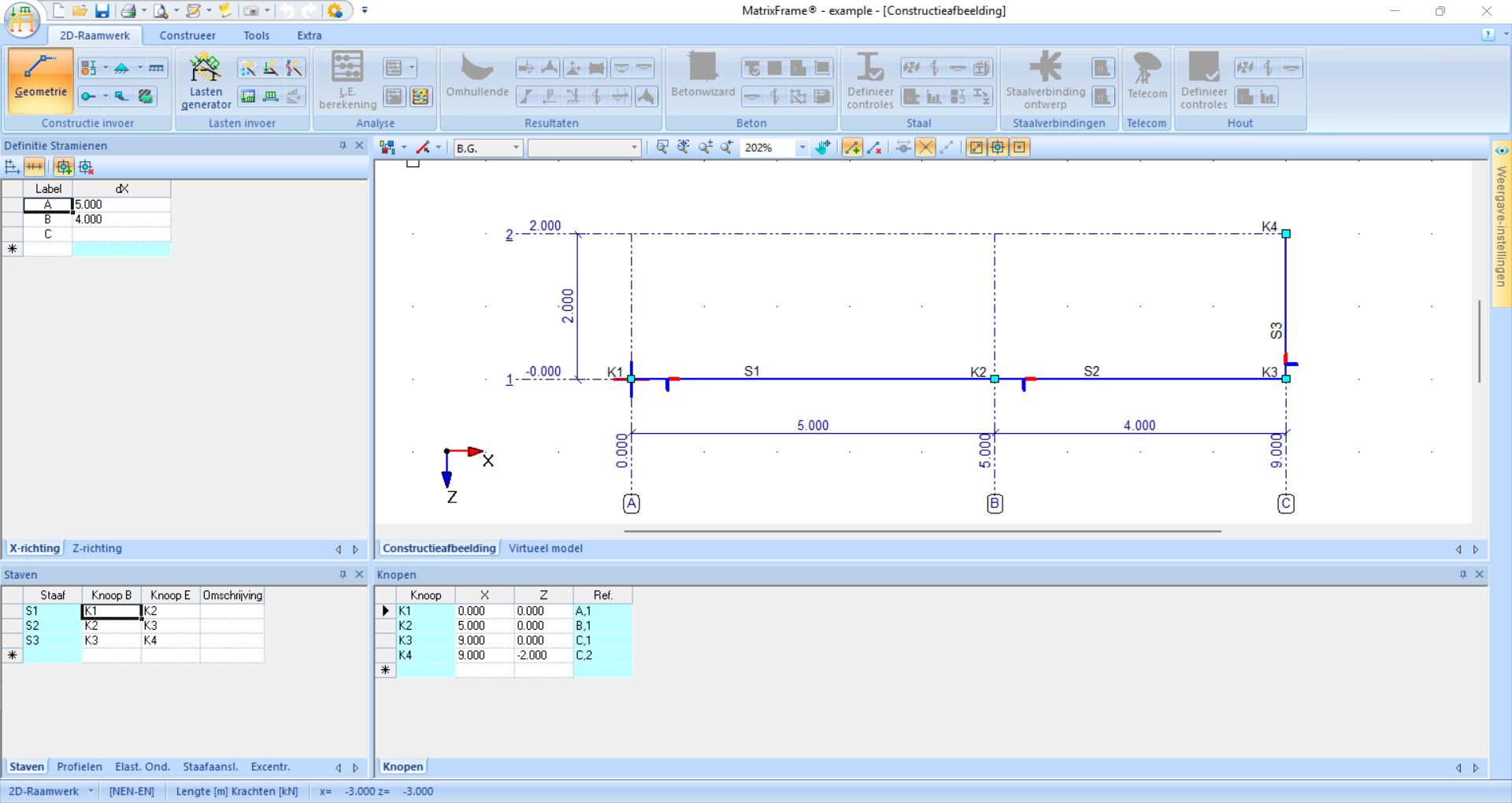
Fig. 42 Voorbeeldconstructie

1. Maak een nieuw project - ‘2D-Raamwerk’ en klik ‘Ok’. De optie ‘1D-ligger’ en ‘2D-vakwerk’ zijn versimpelingen van de ‘2D-Raamwerk’-optie. De optie ‘3D-Raamwerk’ en ‘3D-Vakwerk’ kan je proberen, maar daar krijgt men over het algemeen hoofdpijn van.

   Example

   

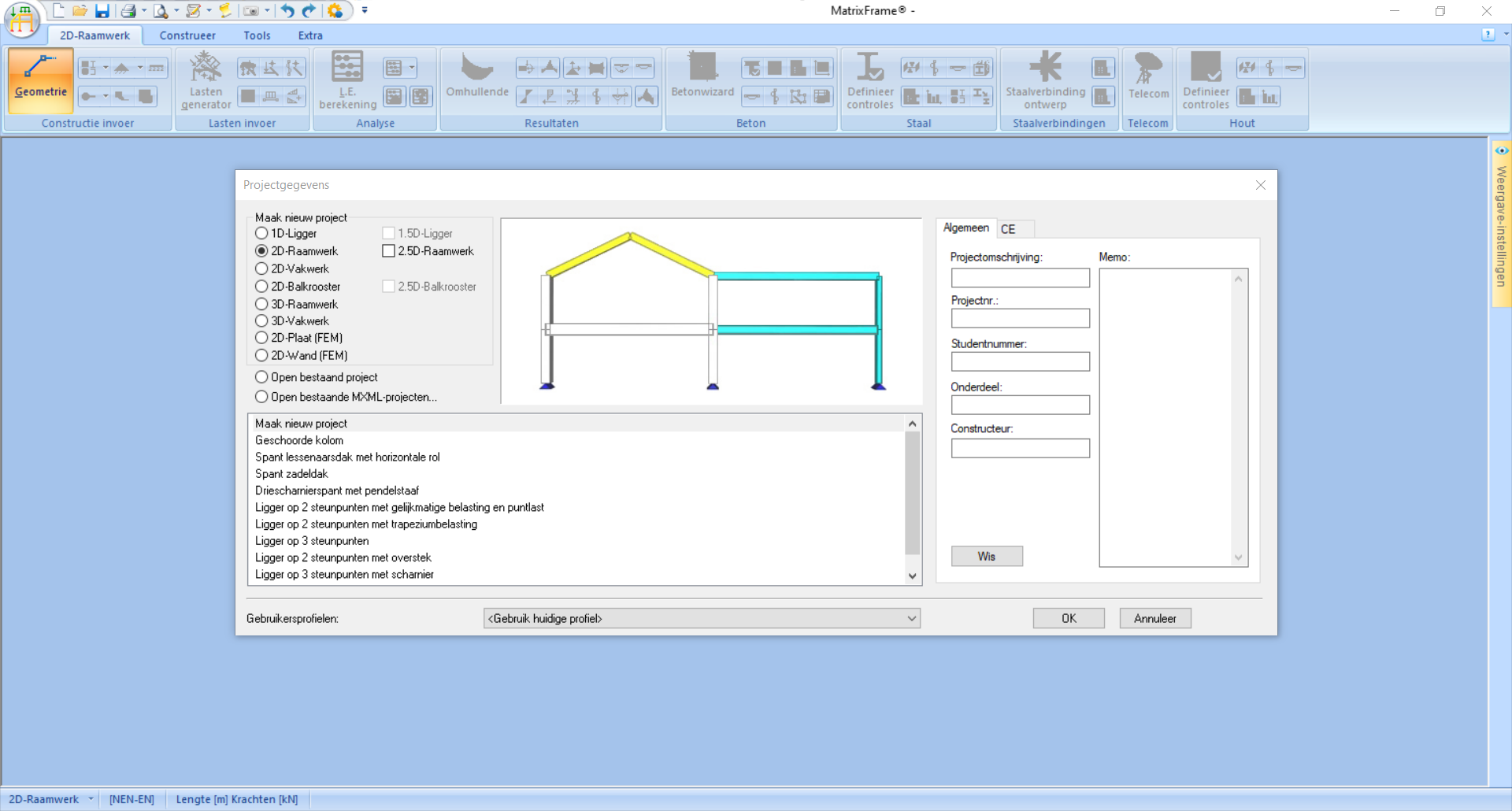
   Fig. 43 Aangezien het hier gaat om een 2D-Raamwerk selecteren we die optie.

2. Je belandt direct in de ‘Geometrie’ interface. Klik in het grid om je geometrie te vormen. De coördinaten zijn zijn zichtbaar in de onderbalk en de afmetingen verschijnen tijdens het klikken. Gebruik Esc op je toetsenbord om te stoppen of op een volgend element te beginnen die niet vastzit aan het uiteinde van het vorige element. Pas eventueel afmetingen aan met behulp van de stramienen aan de linkerkant of de coördinaten aan de onderkant van het scherm.

   Example

   

   Fig. 44 De eerste staaf is al getekend en van de tweede staaf is de coordinaat \(\left(9,0 \right)\) zichtbaar in de balk onderaan.

   

   Fig. 45 Als alle knopen en staven getekend zijn is dit het resultaat

3. Ga verder met de ‘Profielgegevens’ interface. Ook als deze informatie niet bekend is is het invoeren hiervan vereist. Onder ‘Profielen’ - ‘Handmatige invoer’ kan je een \(A\), \(I\) en \(E\) invullen. Het is niet mogelijk een waarde van \(0\) of \(\infty\) in te vullen, daarvoor zal je een kleine of grote numerieke waarde moeten invoeren. Tip, \(\cdot10^6\) kan je invoeren als e6 Vergeet niet op ‘Pas toe op alles’ te klikken! Linksonder in het scherm zie je nu achter elke staaf een profielnaam staan.

   Example

   In dit voorbeeld is er enkel een \(EI\) gegeven, terwijl we een losse \(E\) en \(I\) moeten invoeren. Daarom kan je twee getallen kiezen waarvan het product \(7.8 \cdot 10^4\) is, bijvoorbeeld \(E = 200 \cdot 10^6\) en \(I = 3.9 \cdot 10^-2\). \(EA\) is \(\infty\), waarvoor we een grote numerieke waarde kunnen invoeren, bijvoorbeeld \(A = 10 \cdot 10^3\).

   

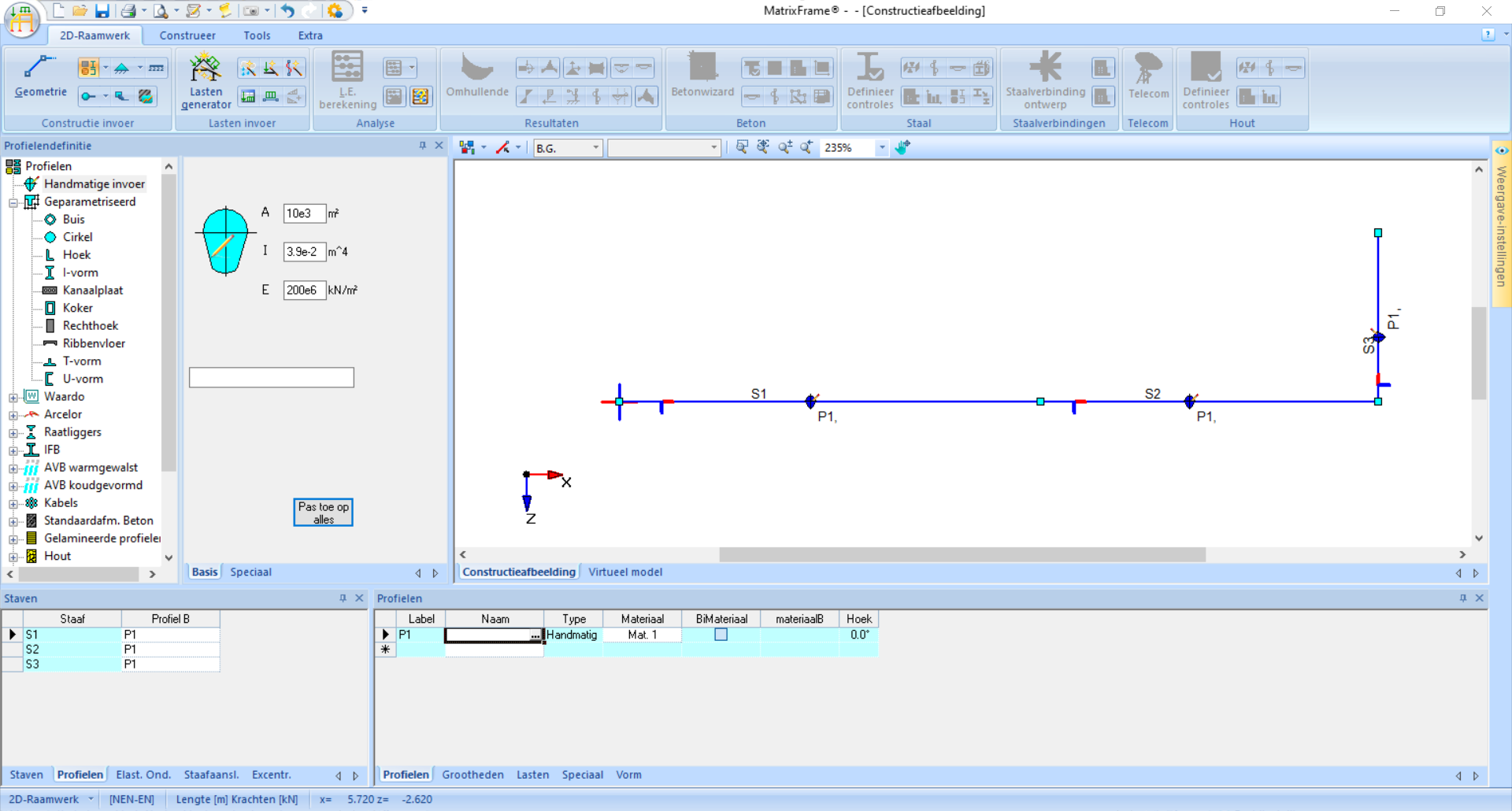
   Fig. 46 Als alles is ingevoerd is dit het resultaat

4. De volgende stap is het toevoegen van opleggingen. Er zijn een aantal standaard opties, maar je kan ook handmatig translatie- en rotatierichtingen vastzetten. De opleggingen kan je plaatsen op de knopen of langs een staaf (in dat geval wordt er een nieuwe knoop gemaakt).

   Example

   

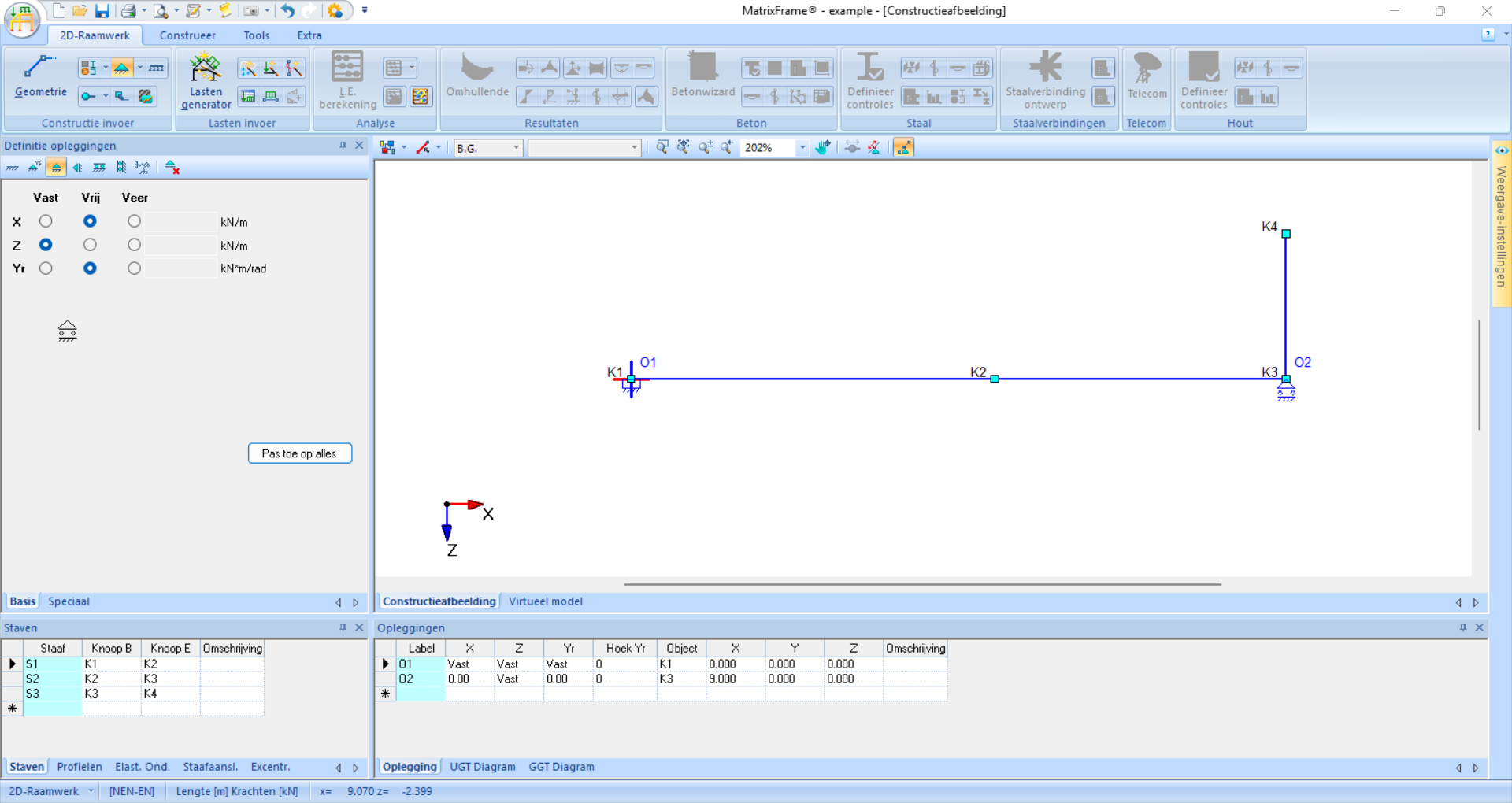
   Fig. 47 De inklemming en roloplegging van het voorbeeld zijn na toevoegen zowel in de grafische weergave als in het onderste venster zichtbaar.

5. Nu kunnen we verder met scharnieren. In een raamwerk is standaard alles momentvast verbonden. Per staaf kan je voor elk uiteinde aangeven of dit een scharnier moet worden door op een deel van die staaf te klikken. Als twee aansluitende staven scharnierend zijn verbonden is het niet nodig om beide staafuiteindes scharnierend te maken, ééntje is genoeg.

   Example

   

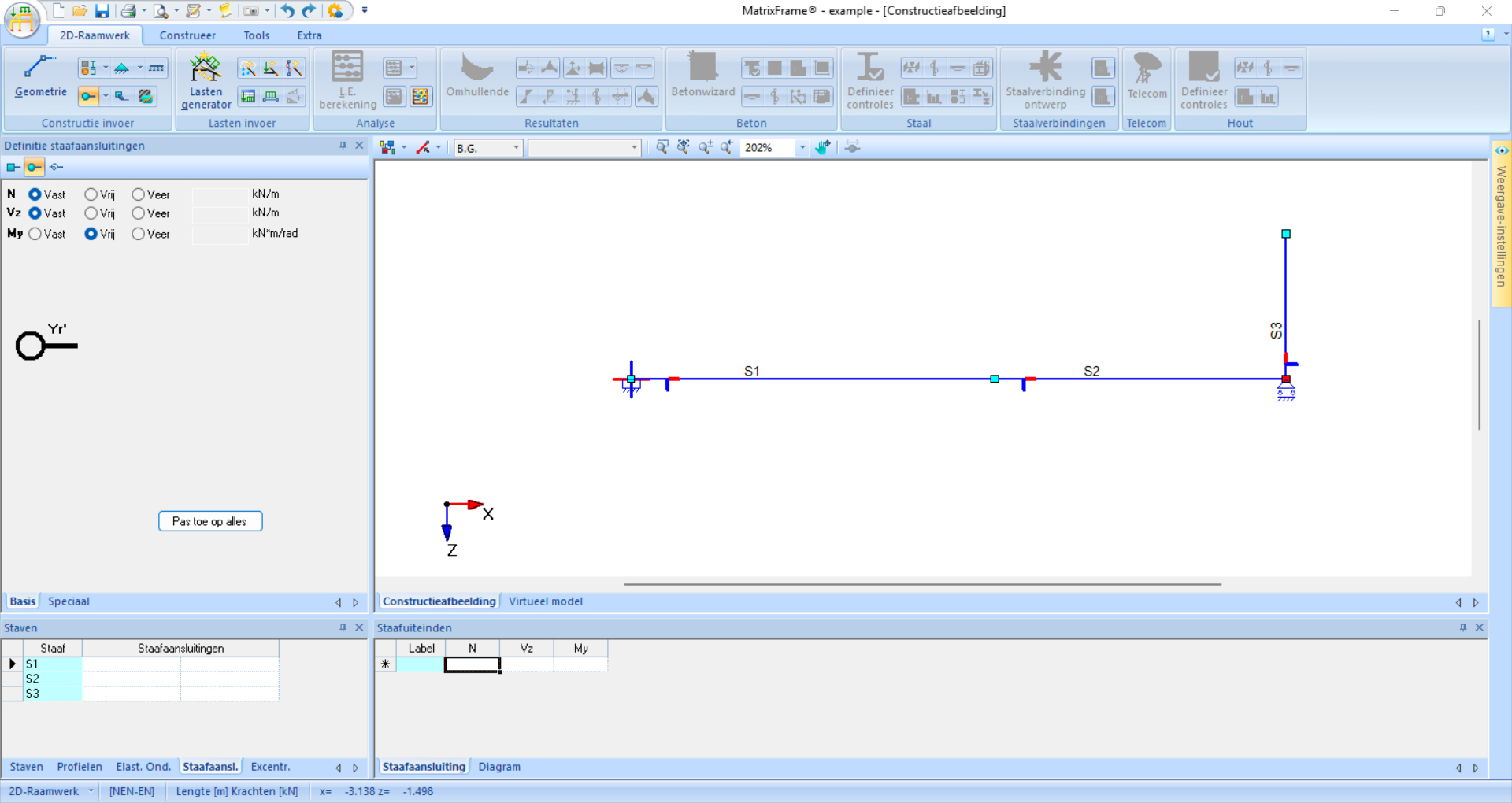
   Fig. 48 In dit voorbeeld zijn er geen scharnieren, dus kan deze stap overgeslagen worden.

6. De laatste configuratiestap is het toevoegen van belastingen. Je kan verschillende belastingsgevallen (B.G.) toevoegen, maar zolang je er maar één hoeft door te rekenen is het niet nodig die opties aan te passen. Voor elke belasting is het wel nodig de waarde en richting aan te geven en de staaf aan te klikken waarop deze last werkt. In het venster onderin het scherm kan je deze ook nog aanpassen.

   Example

   

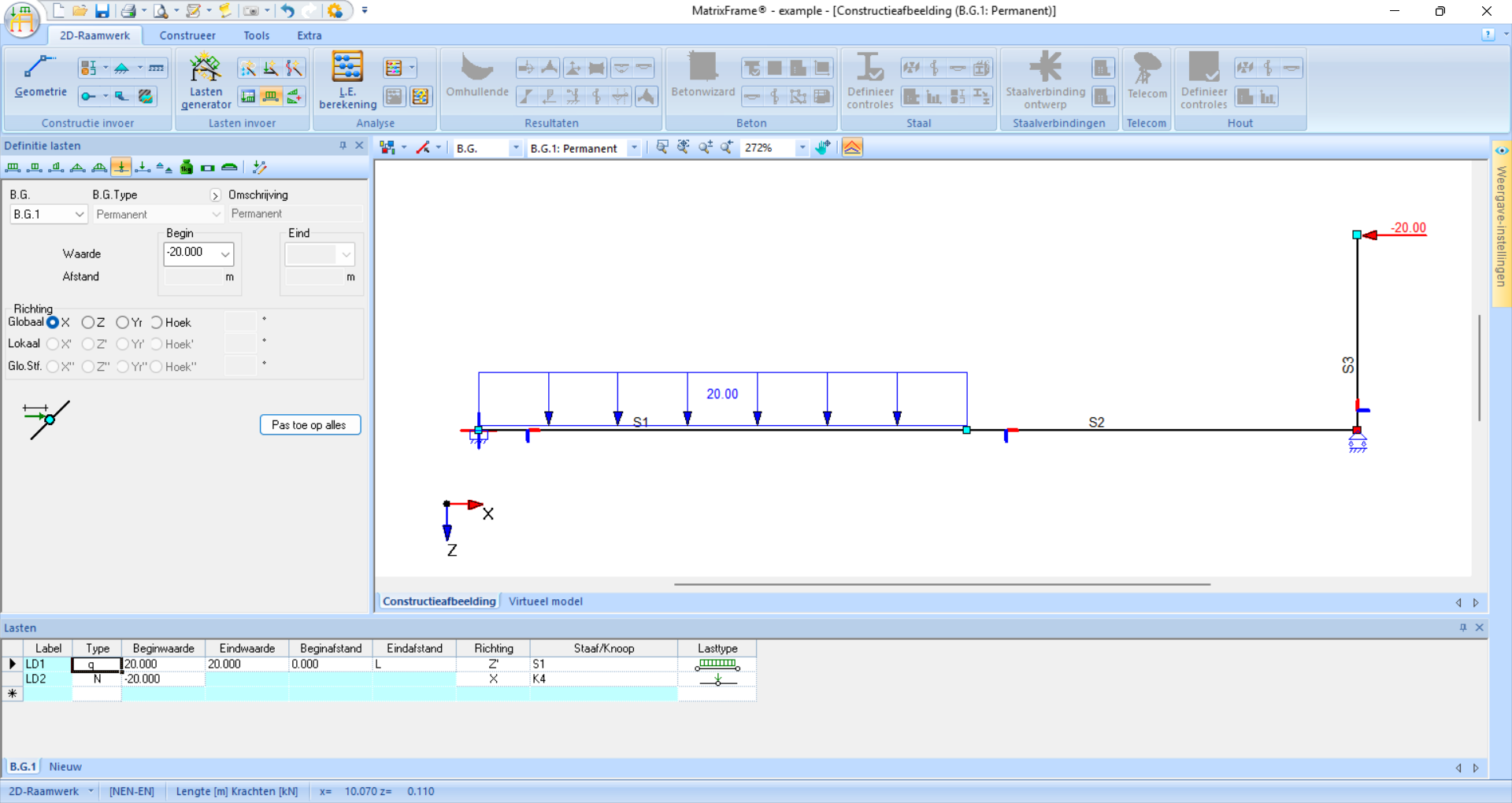
   Fig. 49 In dit voorbeeld zijn er twee belastingen. De verdeelde belasting is aangebracht in de lokale z richting en de puntlast in de globale x-richting met een negatieve waarde zodat die naar links werkt.

7. Nu alles geconfigureerd is kan je op L.E. berekening (linear-elastische berekening) klikken. Er opent zich dan een dialoogvenster die foutmeldingen geeft als er iets niet klopt

   Example

   

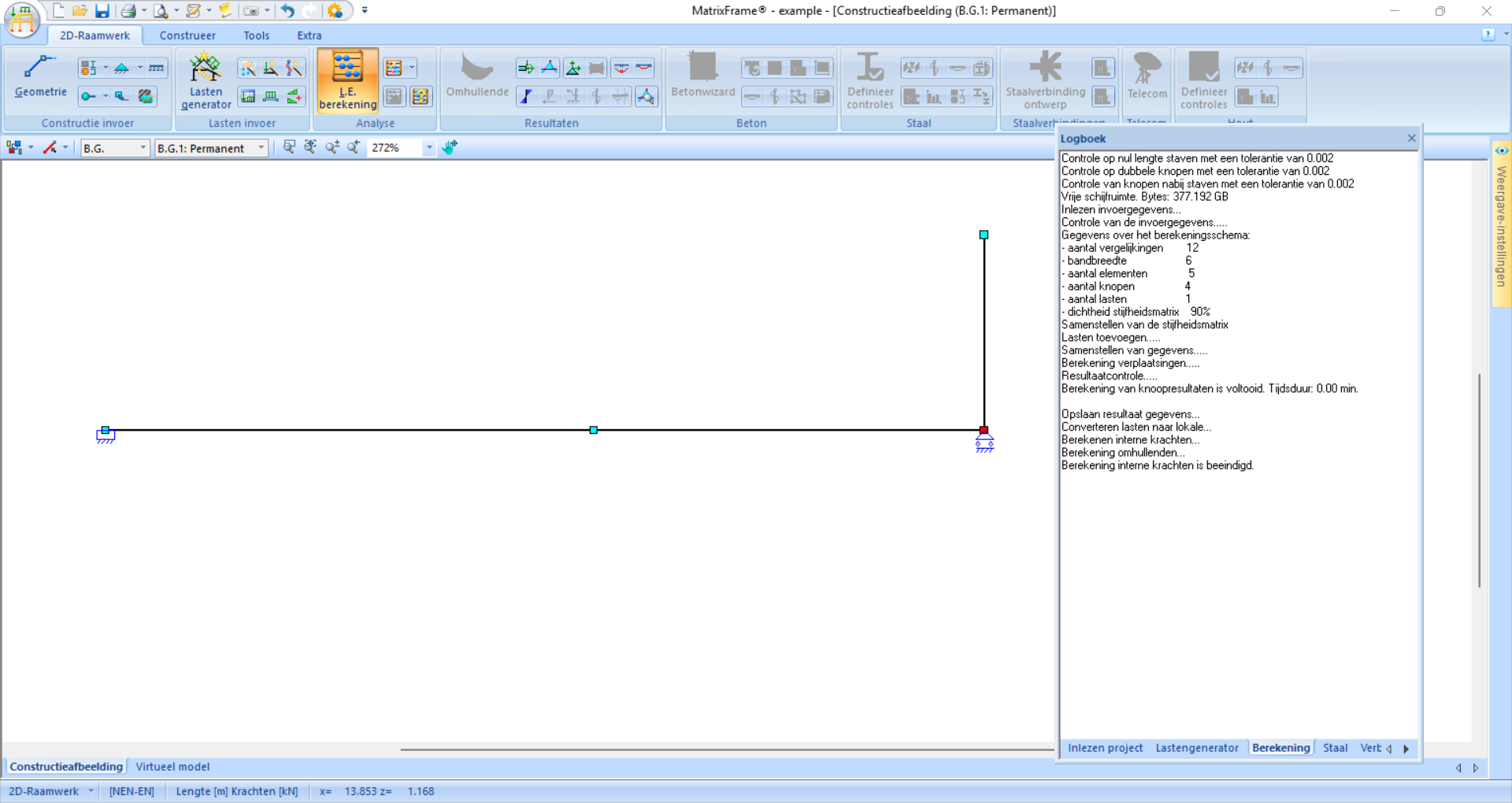
   Fig. 50 In dit voorbeeld is alles goed geconfigureerd en geeft het logboek geen foutmeldingen

8. Om de resultaten te bekijken zijn er een aantal opties. De oplegreacties kunnen los worden getoond. Let op, de richting van de pijlen geeft de daadwerkelijke richting aan van de krachten en koppels; een eventueel minteken geeft aan dat die kracht in de negatieve richting van het assenstelsel werkt.

   Example

   

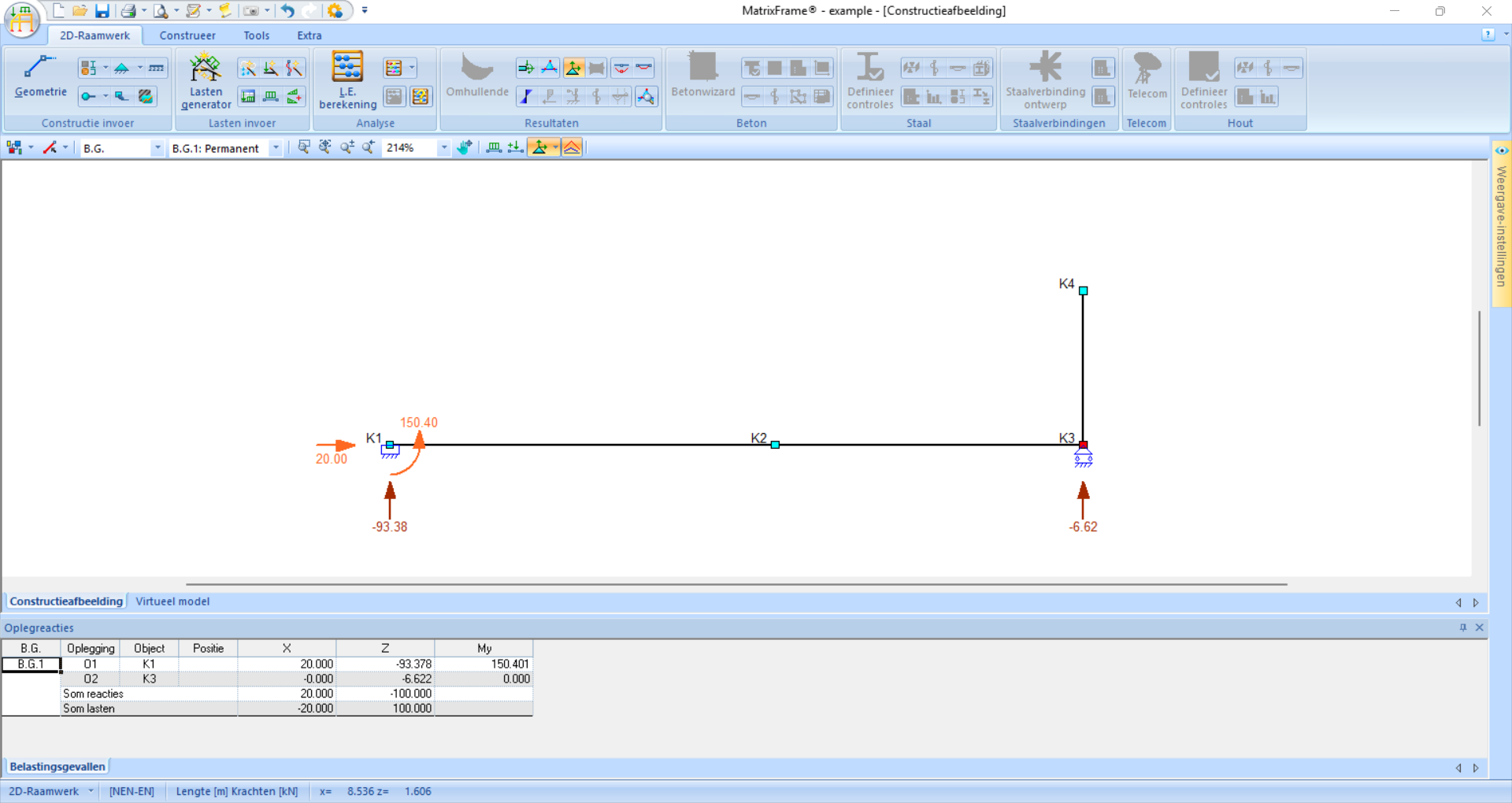
   Fig. 51 In dit voorbeeld zijn vier oplegreacties zichtbaar. De verticale oplegreacties werken naar boven; het minteken geeft aan dat deze in de negatieve z-richting werken.

9. De snedekrachtenlijnen kunnen ook worden getoond. Deze kunnen per snedekracht getoond worden volgens de vervormingstekens zoals we die gewend zijn. Mochten de vervormingstekens niet zichtbaar zijn kan je inzoomen of de schaal vergroten onder ‘Weergave-instellingen’ - ‘Beeldinstellingen’ - ‘Eigenschappen’ - ‘Resultaten’ - ‘Normaalkracht (Nx)’/’Dwarskracht (Vz)’/’Moment (My)’ - ‘Vorm’ - ‘Schaal’ - Voeg waarde in en klik op ‘Toepassen’. Als een staaf wordt aangeklikt zijn links in het scherm alle snedekrachten en verplaatsingen van die staaf zichtbaar. Onderin het scherm worden een aantal karakteristieke waardes getoond. De waardes worden getoond volgens het lokale assenstelsel.

   Example

   

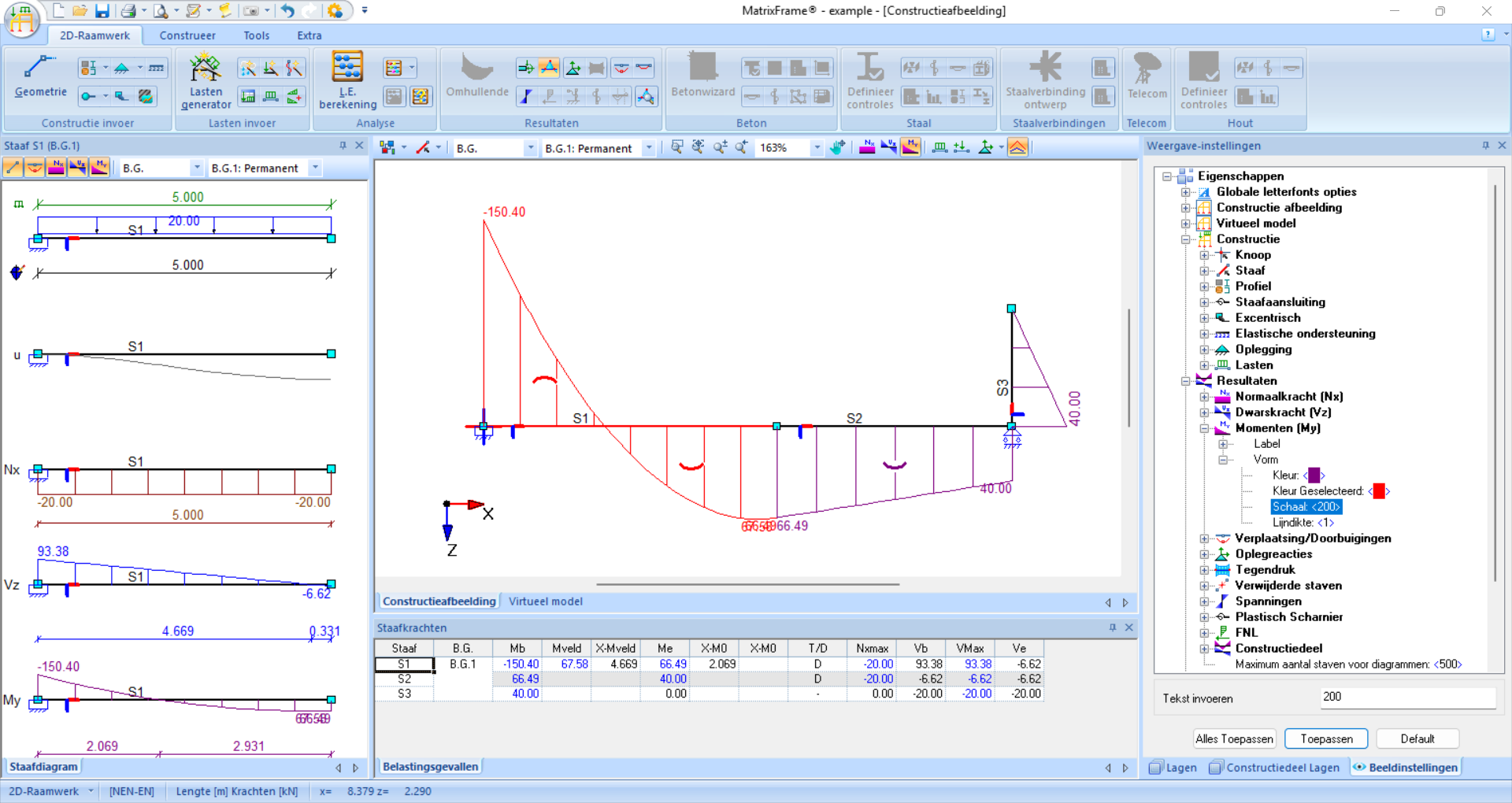
   Fig. 52 De momenten zijn zichtbaar gemaakt met staaf AD in detail aan de linkerkant. De schaal is aangepast zodat de vervormingstekens zichtbaar zijn.

   

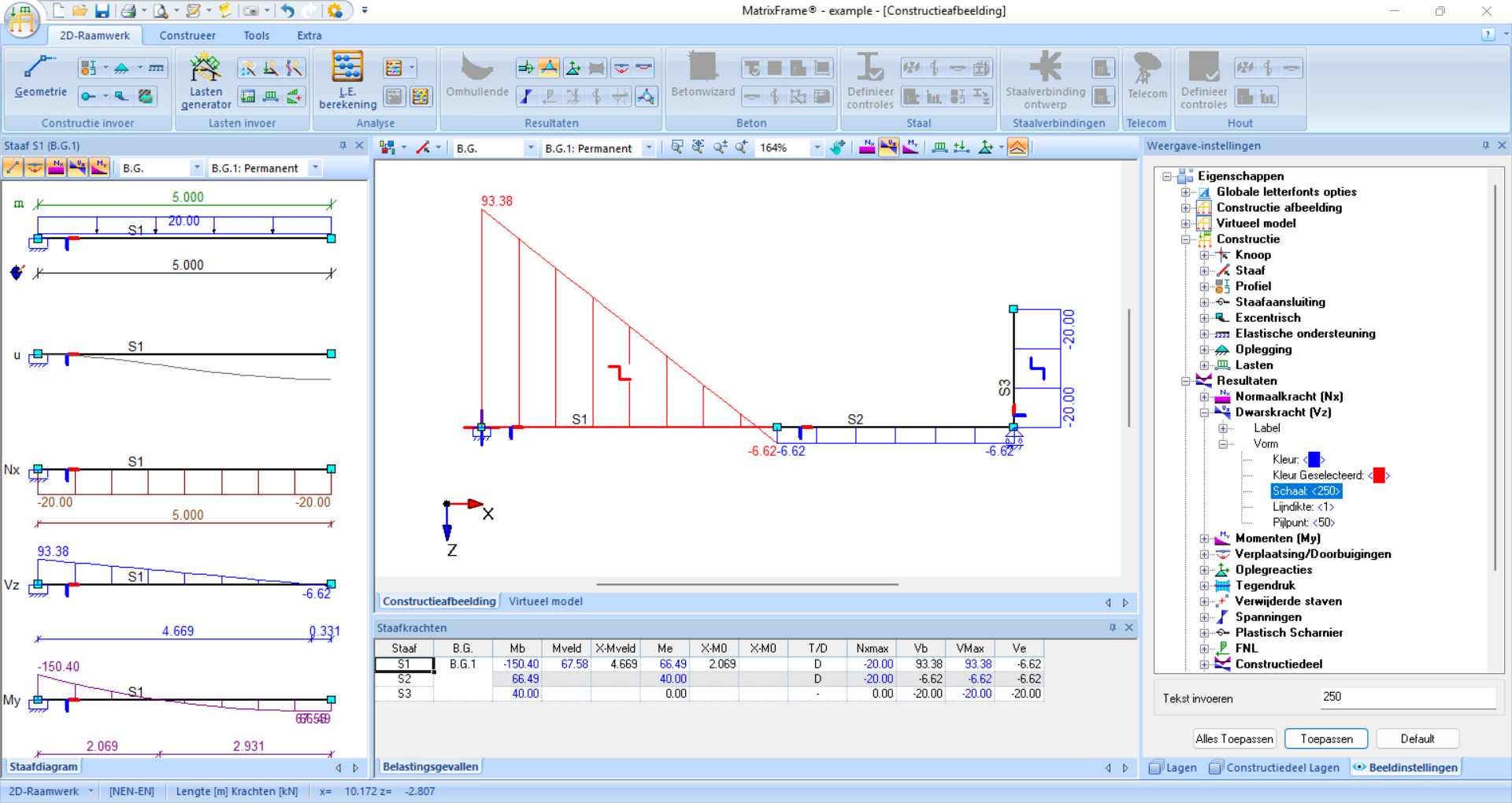
   Fig. 53 Ook de dwarskrachten kunnen worden getoond. Het vervormingsteken van DB is niet zichtbaar in deze weergave, als er verder wordt ingezoomd of de schaal verder wordt vergroot zou die wel zichtbaar worden.

   

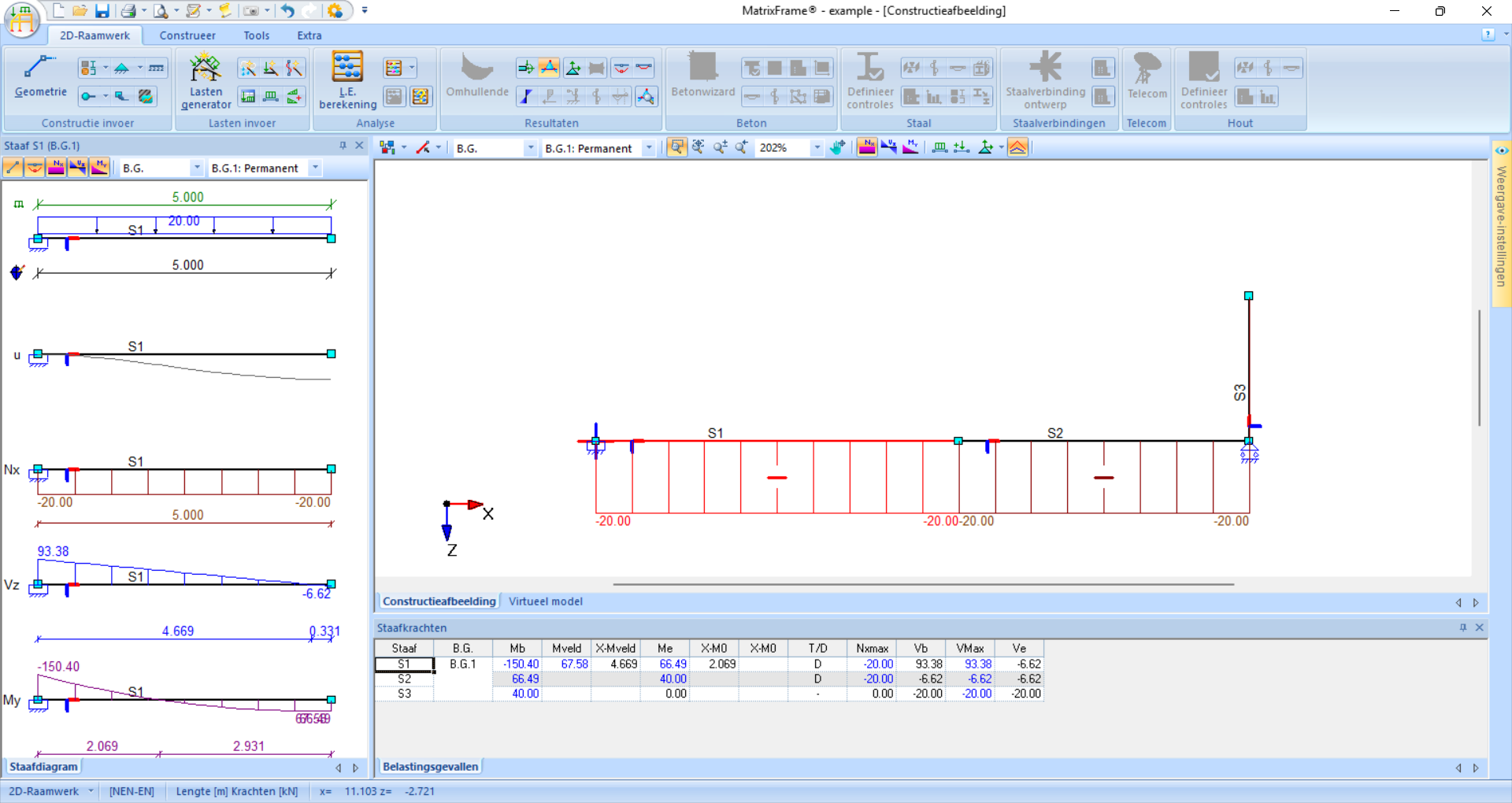
   Fig. 54 De normaalkrachten kunnen ook zichtbaar worden gemaakt.

10. Ook verplaatsingen kunnen worden getoond. Het aantal decimalen kan worden aangepast onder ‘Weergave-instellingen’ - ‘Beeldinstellingen’ - ‘Eigenschappen’ - ‘Resultaten’ - ‘Verplaatsingen/Doorbuigingen’ - ‘Label’ - ‘Decimalen’ - Voeg waarde in en klik op ‘Toepassen’

    Example

    

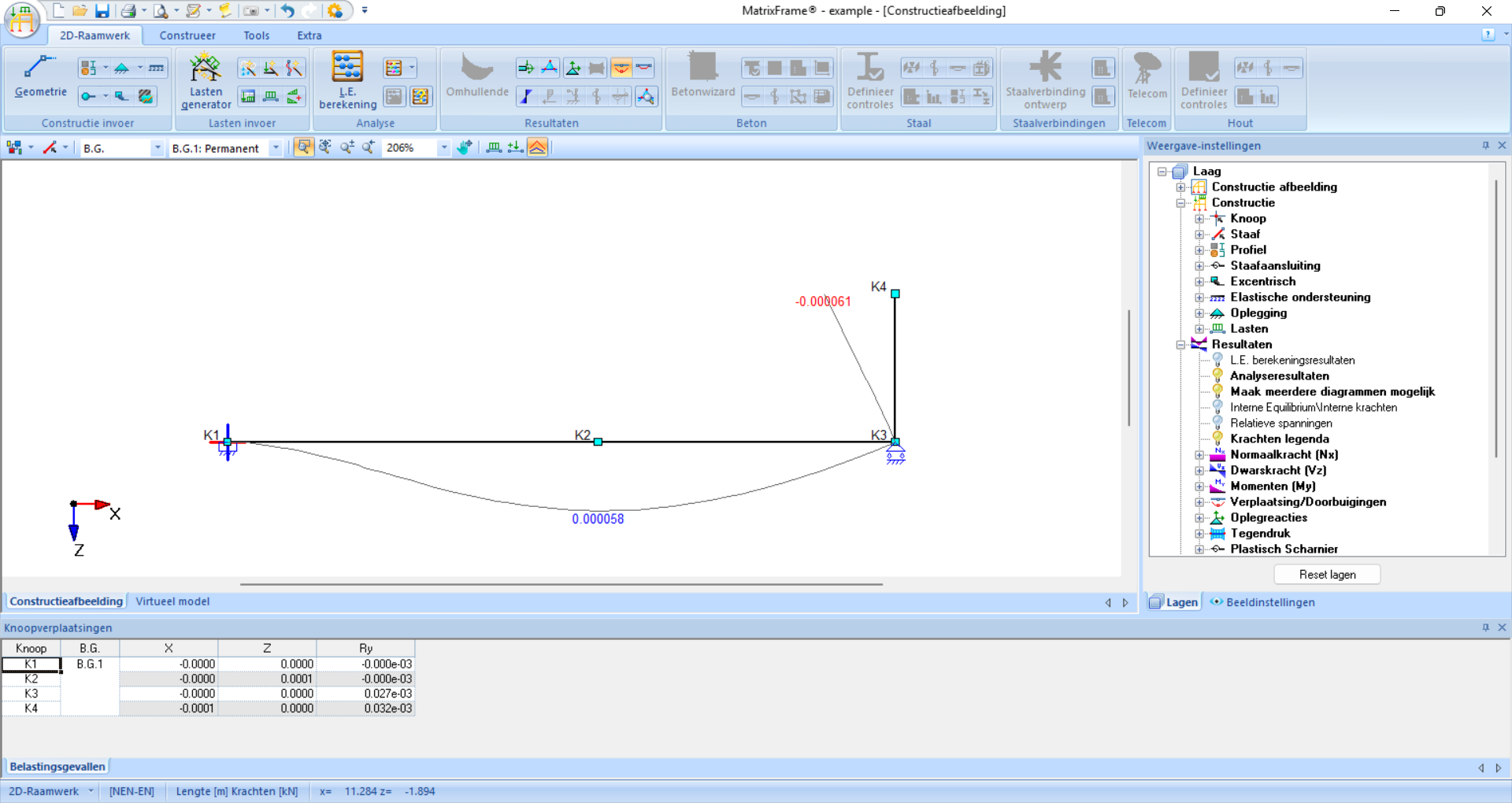
    Fig. 55 De verplaatsingen zijn zichtbaar gemaakt. Het aantal decimalen is aangepast zodat de exacte verplaatsingen kunnen worden gevonden.

11. Tot slot kunnen waardes op specifieke posities worden afgelezen met de spion functie. Klik daarvoor een staaf aan en voer onder ‘Invoer pos:’ een locatie in in het lokale assenstelsel. De tabel en grafische weergave toont dan waardes van snedekrachten en verplaatsingen op dat punt.

    Example

    

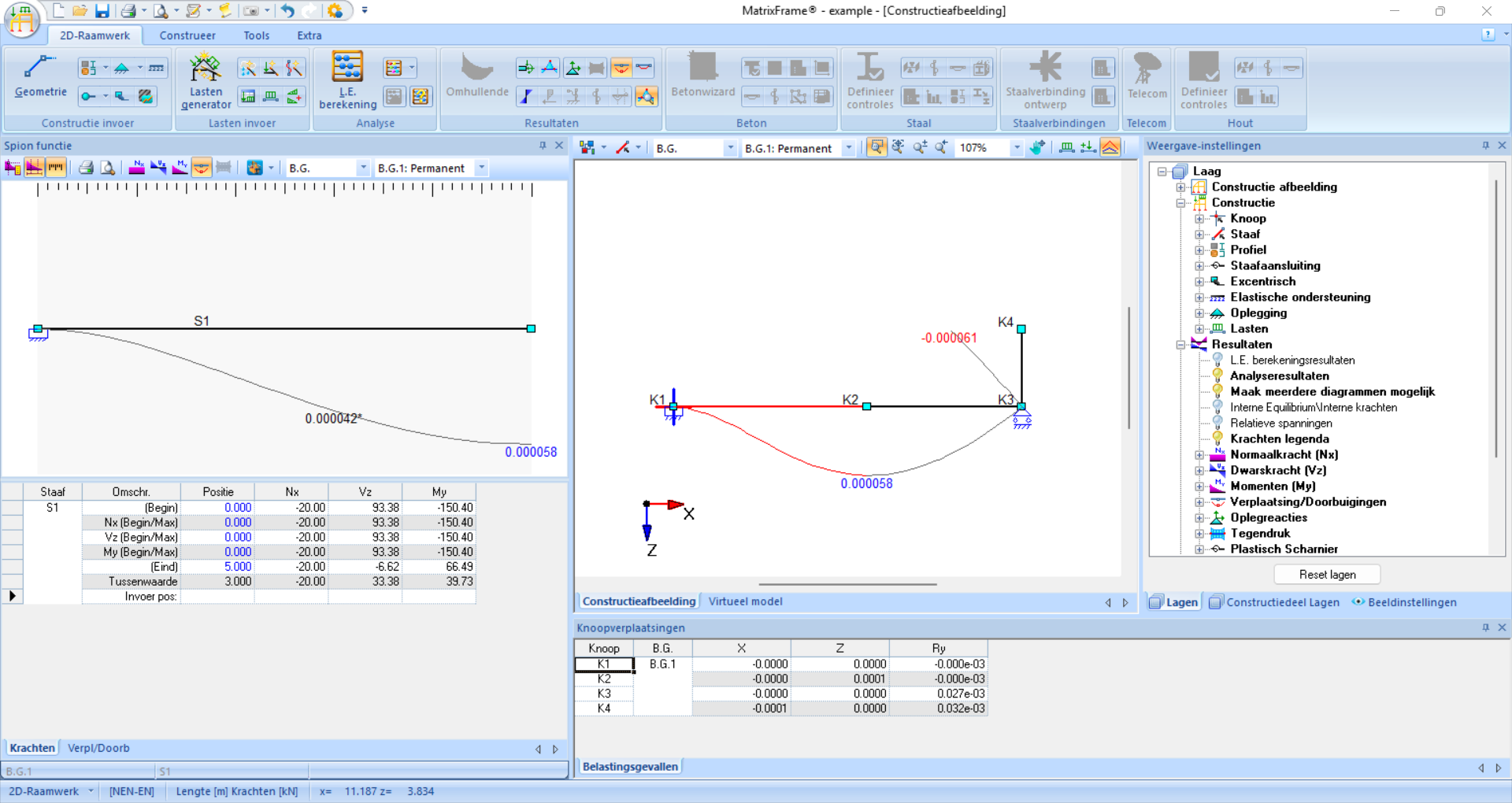
    Fig. 56 Op \(3\) meter rechts van A zijn voor dit voorbeeld de snedekrachten en verplaatsingen bepaald: een verplaatsingen van \(0.000042 \ \rm{m}\), een moment van \(39.73 \ \rm{kNm}\), een dwarskracht van \(33.38 \ \rm{kN}\) en een normaalkracht van \(-20 \ \rm{kN}\).

Example

Het bestand van dit voorbeeld is hier te downloaden.