Voorbeeld 7#
import sympy as sym
import matplotlib.pyplot as plt
import numpy as np
sym.init_printing()
oo = sym.Dummy('oo', prime=True)
very_small = 1/oo
x = sym.symbols('x')
C_1, C_2, C_3, C_4 = sym.symbols('C_1, C_2, C_3, C_4')
A_v, B_v = sym.symbols('A_v, B_v')
ql, Vl, Ml, kappal, phil, wl = sym.symbols('q_z, V, M, kappa, phi, w')
L = 10
F = 35
EI = sym.symbols('EI')
q = A_v * sym.SingularityFunction(x,0,-1) + F * sym.SingularityFunction(x,L/2,-1) + B_v * sym.SingularityFunction(x,L,-1)
display(sym.Eq(ql,q))
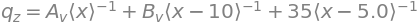
V = -sym.integrate(q, x) + C_1
display(sym.Eq(Vl,V))
M = sym.integrate(V, x) + C_2
display(sym.Eq(Ml,M))
kappa = M/EI + 1/EI*(1-5/x)*sym.SingularityFunction(x,5,0)*(A_v*L/2) + 1/EI*(1-5/x)*sym.SingularityFunction(x,5,1)*(A_v+F)
display(sym.Eq(kappal,kappa))
phi = sym.integrate(kappa, x) + C_3
display(sym.Eq(phil,phi))
w = -sym.integrate(phi, x) + C_4
display(sym.Eq(wl,w))
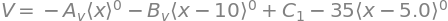
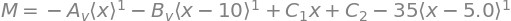
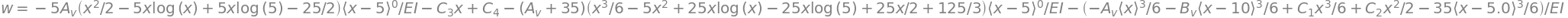
eq1 = sym.Eq(M.subs(x,0),0)
eq2 = sym.Eq(w.subs(x,0-very_small),0).subs(oo,sym.oo)
eq3 = sym.Eq(M.subs(x,L),0)
eq4 = sym.Eq(w.subs(x,L),0)
eq5 = sym.Eq(V.subs(x,0-very_small),0).subs(oo,sym.oo)
eq6 = sym.Eq(V.subs(x,L+very_small),0).subs(oo,sym.oo)
display(eq1, eq2, eq3, eq4, eq5, eq6)
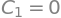
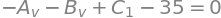
sol = sym.solve((eq1,eq2,eq3,eq4,eq5,eq6),(C_1,C_2,C_3,C_4,A_v,B_v))
display(sol)
display(w.subs(sol).factor(EI))
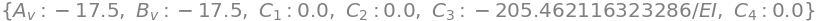
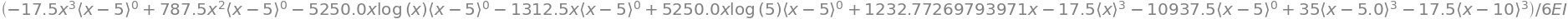
w_numpy = sym.lambdify(x, w.subs(sol).subs(EI,10000).rewrite(sym.Piecewise))
x_numpy = np.linspace(0,L,100)
plt.figure()
plt.plot(x_numpy,w_numpy(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$w$',rotation=0);
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
print(w_numpy(5))
print(w_numpy(7.24562))
0.06627272482830962
0.04665771610574422
<lambdifygenerated-1>:2: RuntimeWarning: divide by zero encountered in log
return 0.0205462116323286*x + 0.00875*((1/2)*x**2 - 5*x*log(x) + 5*x*log(5) - 25/2)*select([greater(x, 5),True], [1,0], default=nan) - 0.00175*((1/6)*x**3 - 5*x**2 + 25*x*log(x) - 25*x*log(5) + (25/2)*x + 125/3)*select([greater(x, 5),True], [1,0], default=nan) - 0.000291666666666667*select([greater(x, 0),True], [x**3,0], default=nan) + (7/12000)*select([greater(x - 5.0, 0),True], [125.0*(0.2*x - 1)**3,0], default=nan) - 0.000291666666666667*select([greater(x, 10),True], [(x - 10)**3,0], default=nan)
<lambdifygenerated-1>:2: RuntimeWarning: invalid value encountered in multiply
return 0.0205462116323286*x + 0.00875*((1/2)*x**2 - 5*x*log(x) + 5*x*log(5) - 25/2)*select([greater(x, 5),True], [1,0], default=nan) - 0.00175*((1/6)*x**3 - 5*x**2 + 25*x*log(x) - 25*x*log(5) + (25/2)*x + 125/3)*select([greater(x, 5),True], [1,0], default=nan) - 0.000291666666666667*select([greater(x, 0),True], [x**3,0], default=nan) + (7/12000)*select([greater(x - 5.0, 0),True], [125.0*(0.2*x - 1)**3,0], default=nan) - 0.000291666666666667*select([greater(x, 10),True], [(x - 10)**3,0], default=nan)
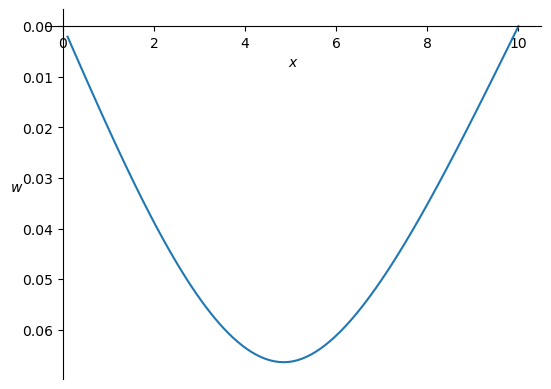
V_numpy = sym.lambdify(x, V.subs(sol).subs(EI,10000).rewrite(sym.Piecewise))
x_numpy = np.linspace(0,L,100)
plt.figure()
plt.plot(x_numpy,V_numpy(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$V$',rotation=0);
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
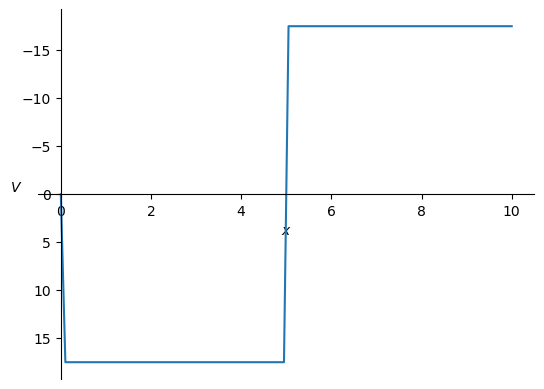
M_numpy = sym.lambdify(x, M.subs(sol).subs(EI,10000).rewrite(sym.Piecewise))
x_numpy = np.linspace(0,L,100)
plt.figure()
plt.plot(x_numpy,M_numpy(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$M$',rotation=0);
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
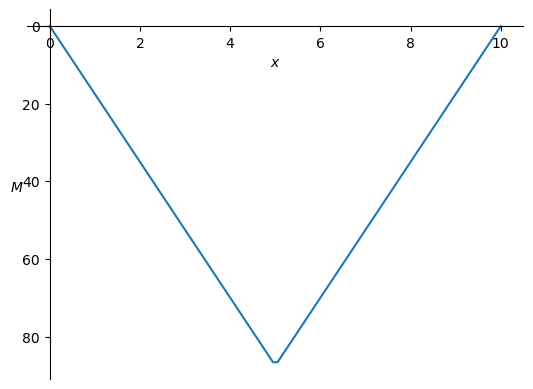
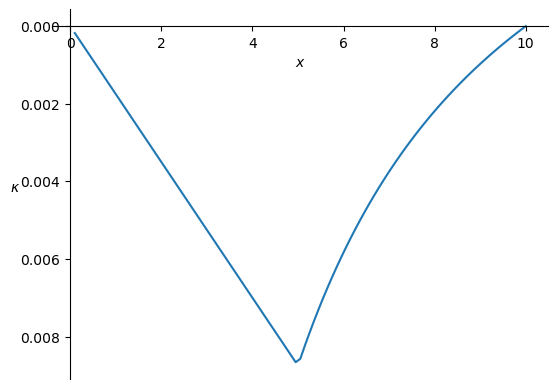
kappa_numpy = sym.lambdify(x, kappa.subs(sol).subs(EI,10000).rewrite(sym.Piecewise))
x_numpy = np.linspace(0,L,100)
plt.figure()
plt.plot(x_numpy,kappa_numpy(x_numpy))
# plt.plot(x_numpy, a1(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$\kappa$',rotation=0);
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
<lambdifygenerated-4>:2: RuntimeWarning: divide by zero encountered in divide
return -0.00875*(1 - 5/x)*select([greater(x, 5),True], [1,0], default=nan) + 0.00175*(1 - 5/x)*select([greater(x, 5),True], [x - 5,0], default=nan) + 0.00175*select([greater(x, 0),True], [x,0], default=nan) + 0.00175*select([greater(x, 10),True], [x - 10,0], default=nan) - 7/2000*select([greater(x - 5.0, 0),True], [x - 5.0,0], default=nan)
<lambdifygenerated-4>:2: RuntimeWarning: invalid value encountered in multiply
return -0.00875*(1 - 5/x)*select([greater(x, 5),True], [1,0], default=nan) + 0.00175*(1 - 5/x)*select([greater(x, 5),True], [x - 5,0], default=nan) + 0.00175*select([greater(x, 0),True], [x,0], default=nan) + 0.00175*select([greater(x, 10),True], [x - 10,0], default=nan) - 7/2000*select([greater(x - 5.0, 0),True], [x - 5.0,0], default=nan)
