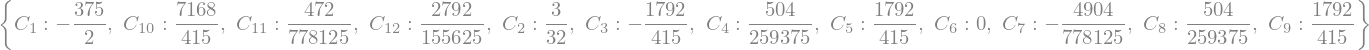import matplotlib
if not hasattr(matplotlib.RcParams, "_get"):
matplotlib.RcParams._get = dict.get
Lesson Monday September 9th#
During today’s lesson it’s demonstrated how you to use differential equations to solve structural problems.
Demonstration#
Given a structure as shown below:
We can calculate the force distribution and displacements of this structure using differential equations.
First, let’s define the segments with continuous loads. This requires splitting the top element DB into two because the distributed load causes a discontinuity. This leads to four segments:
AC
AD
DE
EB
Now, each segment can be drawn separately, indicating the loads, coordinate systems, dimensions and section forces at the edges of each segment.
Element AC#
As element is hinged at both ends and is only loaded at its end, it’s a zero-force member. The free-body diagram therefore only includes normal forces:
Fig. 1 Free body diagram element AC#
As this element is unloaded, the loading equation for this element gives:
leading to the equations:
Because of the support at C the first boundary condition is as follows:
At C the normal force is unknown (equilibrium with support reactions).
At A the extension is unknown as A can move horizontally this leads to a potential displacement of A in the longitudinal direction of the element.
The normal force at A follows from the equilibrium of node A. It’s free-body-diagram is:
Fig. 2 Free body diagram node A#
Horizontal equilibrium gives the second boundary condition:
This element could be solved independently as there are two unknowns (two integration constants) and two equations ((1) and (2)).
Element AD#
Again, this element is a zero-force member. The free-body diagram therefore only includes normal forces:
Fig. 3 Free body diagram element AD#
As this element is unloaded too, the load equation for this element gives:
leading to the equations:
Because of the support at A the first boundary condition is as follows:
At D another boundary condition can be identified from the consistency of displacements: the downwards displacement of the top of element AD must be the same as the downwards displacement of the left of element DE:
And finally, a boundary condition can be formulated as the normal force in D is in equilibrium with the forces from element DE. The free-body-diagram of D is:
Fig. 4 Free body diagram node D#
Vertical equilibrium gives:
Element DE#
The free-body diagram of this element is:
Fig. 5 Free body diagram element DE#
As this element is unloaded, the load equation for this element gives:
leading to the equations:
Because of the hinge at D, a boundary condition can be formulated as:
At E another boundary condition can be identified from the consistency of displacements: both the downwards and rotational displacement of the right of element DE must be the same as the downwards and rotational displacement of the left of element BE:
Finally, there should be consistency with the section forces too, as shown in the free body diagram:
Fig. 6 Free body diagram node E#
Vertical equilibrium gives:
Moment equilibrium gives:
Element BE#
The free-body diagram of this element is:
Fig. 7 Free body diagram element BE#
As this element is loaded, the load equation for this element gives:
leading to the equations:
Because of the support at D, two boundary conditions can be formulated directly:
Solve system of equations#
12 boundary conditions have been formulated with 12 integration constants. These can now be solved. You’re advised to use your calculator or a symbolic programming tool to solve this.
Filling in the boundary conditions gives:
Solving this gives:
Now, the full force distribution and displacements of the structure has been solved. For example the moment distribution in BE is \(- 5 \cdot x^{2} + \cfrac{1792}{415} \cdot x + \cfrac{7168}{415}\) which can be plotted as:
Solve using digital tools#
To solve the system of equations using numerical tools, you can write down the equations as a matrix formulation \(Ax=b\) which can easily be solved by ie. your graphical calculator or python.
np.linalg.solve(A,b)
array([[-1.87500000e+02],
[ 9.37500000e-02],
[-4.31807229e+00],
[ 1.94313253e-03],
[ 4.31807229e+00],
[ 0.00000000e+00],
[-6.30232932e-03],
[ 1.94313253e-03],
[ 4.31807229e+00],
[ 1.72722892e+01],
[ 6.06586345e-04],
[ 1.79405622e-02]])
Alternatively, a symbolic programming language can be used to solve the equations exactly. As an example the sympy package in Python is used:
import sympy as sym
sym.init_printing()
x = sym.symbols('x')
q = 10
EI = 5000
EA = 20000
F = 150
q_AC = 0
q_AD = 0
q_CD = 0
q_DE = 0
q_EB = q
C_1, C_2 = sym.symbols('C_1 C_2')
C_3, C_4 = sym.symbols('C_3 C_4')
C_5, C_6, C_7, C_8 = sym.symbols('C_5 C_6 C_7 C_8')
C_9, C_10, C_11, C_12 = sym.symbols('C_9 C_10 C_11 C_12')
N_AC = -sym.integrate(q_AC, x) + C_1
eps_AC = N_AC/EA
u_AC = sym.integrate(eps_AC, x) + C_2
N_AD = -sym.integrate(q_AD, x) + C_3
eps_AD = N_AD/EA
u_AD = sym.integrate(eps_AD, x) + C_4
V_DE = -sym.integrate(q_DE, x) + C_5
M_DE = sym.integrate(V_DE, x) + C_6
kappa_DE = M_DE/EI
phi_DE = sym.integrate(kappa_DE, x) + C_7
w_DE = -sym.integrate(phi_DE, x) + C_8
V_EB = -sym.integrate(q_EB, x) + C_9
M_EB = sym.integrate(V_EB, x) + C_10
kappa_EB = M_EB/EI
phi_EB = sym.integrate(kappa_EB, x) + C_11
w_EB = -sym.integrate(phi_EB, x) + C_12
eq1 = sym.Eq(u_AC.subs(x,10),0)
eq2 = sym.Eq(F + N_AC.subs(x,0)/5*4,0)
eq3 = sym.Eq(u_AD.subs(x,9),0)
eq4 = sym.Eq(w_DE.subs(x,0)-u_AD.subs(x,0),0)
eq5 = sym.Eq(V_DE.subs(x,0) + N_AD.subs(x,0),0)
eq6 = sym.Eq(M_DE.subs(x,0),0)
eq7 = sym.Eq(w_EB.subs(x,0)-w_DE.subs(x,4),0)
eq8 = sym.Eq(phi_EB.subs(x,0)-phi_DE.subs(x,4),0)
eq9 = sym.Eq(V_EB.subs(x,0) - V_DE.subs(x,4),0)
eq10 = sym.Eq(M_EB.subs(x,0) - M_DE.subs(x,4),0)
eq11 = sym.Eq(phi_EB.subs(x,4),0)
eq12 = sym.Eq(w_EB.subs(x,4),0)
sol = sym.solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8,eq9,eq10,eq11,eq12],(C_1,C_2,C_3,C_4,C_5,C_6,C_7,C_8,C_9,C_10,C_11,C_12))
display(sol)