Instructie

De vorige keer hebben we gekeken naar schuifspanningen in rechthoekige doorsnedes. In deze instructie breiden we dat uit naar schuifspanningen in algemene dikwandige doorsnedes.

Relatie met elasticiteitstheorie

Onze schuifspanningsmodel is gebaseerd op een aantal aannames om van snedekrachten naar spanningen te komen. Een meer geavanceerde manier om spanningen in constructies te bepalen is met (complexe) elasticiteitstheorie. Vaak wordt die theorie opgelost met computersimulaties, waarmee spanningen op elk punt in de doorsnede kunnen worden bepaald. Deze simulaties kunnen de beperkingen van ons model bevestigen.

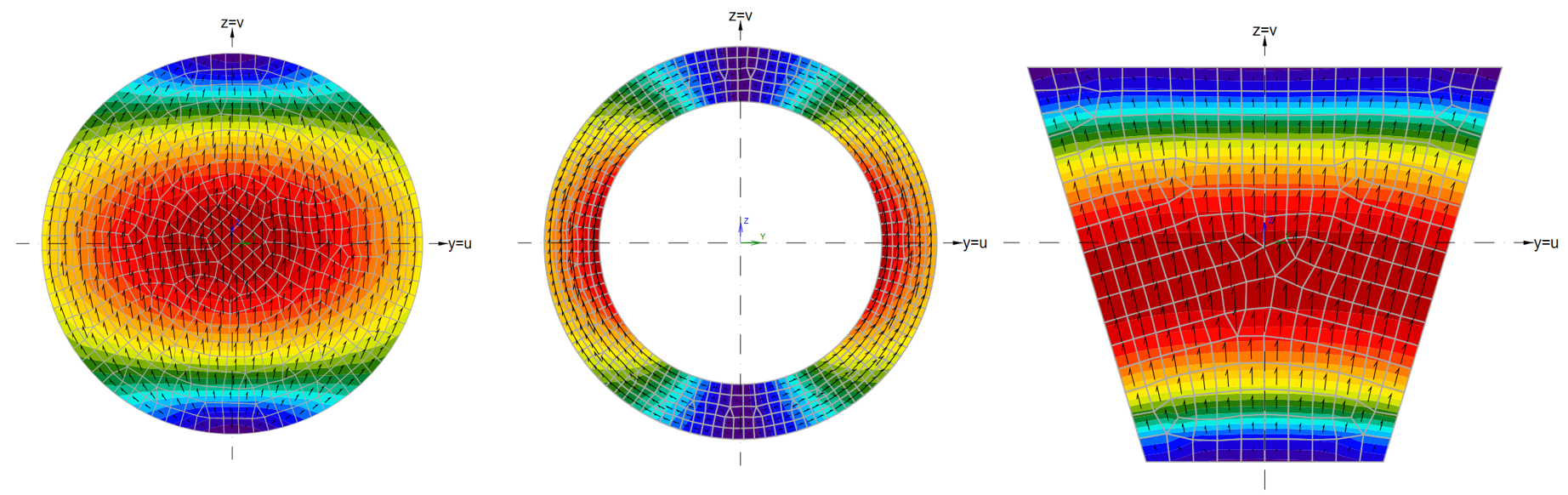
Fig. 22 Voorbeeld van simulatie op basis van elasticiteitstheorie op doorsnedeniveau. De vectoren geven de richting aan van de schuifspanningen en de kleur en grootte de absolute waarde (donkerblauw lage waarde, donkerrood hoge waarde).
Auteur: IDEA StatiCa | Licentie: Alle rechten voorbehouden | Auteursrecht: © IDEA StatiCa 2009-2025 | Bron: https://www.ideastatica.com/support-center/shear-in-rcs-circular-cross-sections

Implicaties model schuifspanningen voor niet-rechthoekige dikwandige doorsneden

Beperkingen van het model

Tijdens de afleiding van de schuifspanningsformule had ons model een aantal aannames. Voor niet-rechthoekige doorsnedes komen daar nog een aantal bij.

De eerdere aanname waarmee ons model alleen geldig is als de schuifspanningen evenredig verdeeld zijn over het afschuifvlak is voor niet-rechthoekige doorsnedes ook van belang vanwege de variatie in afschuivende delen. Voor elk afschuivend deel geldt dat het model alleen geldig is als de breedte van de het afschuivend deel veel kleiner is dan de hoogte van de afschuivend deel. Voor niet-rechthoekige doorsneden, die verschillende delen kunnen hebben met verschillende breedte-hoogte verhoudingen, kan deze aanname dus ook zorgen voor een ongeldig model voor een deel van de doorsnede.

Fig. 23 Voor samengestelde doorsneden is het schuifspanningsmodel alleen geldig in de afschuivende delen waar \(h \gg b\) geldt. In deze doorsnede is dat alleen in het lijf.

De overgangen van verschillende delen van een doorsnede zijn echter ook problematisch. Uit elasticiteitstheorie blijkt namelijk dat bij overgangen in breedte de schuifspanningen niet meer evenredig verdeeld.

Fig. 24 In de getoonde afschuifvlakken zitten dicht bij een (plotselinge) overgang in de breedte van de doorsnede. De schuifspanningen zijn daar dus niet evenredig verdeeld.

Daarnaast heeft de observatie dat de schuifspanningen dwars op de vrije randen van een doorsnede nul moeten zijn ook invloed op de geldigheid van ons model voor niet-rechthoekige doorsneden. Ons model geeft schuifspanning in de richting loodrecht op het afschuifvlak, maar als de randen van de doorsnede niet in diezelfde lopen loopt een component van de schuifspanning in de richting van de vrije rand. Die component moet daar nul zijn, wat niet gegarandeerd is met ons model.

Fig. 25 Links de schuifspanningen volgens ons model met horizontale afschuifvlakken, rechts nulspanningen getoond loodrecht op de vrije randen. Op diagonale randen kunnen deze spanningen niet matchen, waarmee het model dus ongeldig is.

Daarmee kunnen we de schuifspanningsformule voor dikwandige doorsneden dus alleen toepassen op afschuivende vlakken die:

• Door delen waar de breedte veel kleiner is dan de hoogte

• Ver af liggen van overgangen in breedte van de doorsnede

• Waarvan de vrije randen niet loodrecht op de afschuifvlakken lopen.

Als niet aan deze voorwaarden wordt voldaan zou wel een totale kracht kunnen worden gevonden die moet worden overgedragen in het afschuivend vlak, maar de verdeling van de schuifspanningen in dat vlak kan niet worden bepaald met de schuifspanningsformule.

Schuifspanningen in andere richtingen

Niet-rechthoekige doorsnedes zouden kunnen voldoen aan alle aannames, maar niet in de \(y\)- of \(z\)-richting. Als er een afschuifvlak wordt genomen dat niet loodrecht op de \(z\)-as staat, bijvoorbeeld een verticaal afschuifvlak in het \(y,z\)-vlak, dan kan ons schuifspanningsmodel ook worden toegepast. Net zoals voorheen moet het afschuifvlak loodrecht op de randen worden genomen. De schuifspanning die dan wordt berekend is de schuifspanning loodrecht op het snedevlak en evenwijdig aan de rand, maar dus niet per sé in de \(z\)-richting.

Fig. 26 Afschuifvlakken in verschillende richtingen, maar altijd loodrecht op de rand

Voor verticale afschuifvlakken (in horizontale doorsnededelen) geldt dat de schuifspanningen linear verlopen over de ‘hoogte’ (in horizontale richting) van het constructiedeel, mits de breedte van het afschuifvlak constant blijft. Dit kan op vergelijkbare wijze worden afgeleid als het parabolisch verband wat werd gevonden voor horizontale afschuifvlakken in verticale delen.

Volledige afleiding

Om het schuifspanningsverloop te bepalen, kunnen we de formule voor de gemiddelde schuifspanning herschrijven door het statisch moment uit te werken voor een constante breedte:

\[\begin{split} \begin{align*} \tau_{\rm{gem}} &= -\cfrac{V_z \, S_{z}^{\rm{a}}}{b \, I_{zz}} \\ \tau_{\rm{gem}} &= -\cfrac{V_z \, \int_{A^{\rm{a}}} z \, dA^{\rm{a}} }{b \, I_{zz}} \\ \tau_{\rm{gem}} &= -\cfrac{V_z \, z \int_{A^{\rm{a}}} \, dA^{\rm{a}} }{b \, I_{zz}} \\ \tau_{\rm{gem}} &= -\cfrac{V_z \, z \, A^{\rm{a}}}{b \, I_{zz}} \end{align*} \end{split}\]

Het statisch moment is dus niet afhankelijk van \(z\), waarmee de spanning alleen maar toeneemt door de lineair toenemende waarde van \(A^{\rm{a}}\).

In plaats van \(h \gg b\) geldt voor gekromde delen van de constructie dat \(R \gg b\) moet gelden, met \(R\) de straal van kromming van het gekromde deel.

Fig. 27 De voorwaarde \(R \gg b\) moet gelden voor gekromde delen van de doorsnede om een evenredige schuifspanningsverdeling te garanderen.

In theorie zouden ook niet-vlakke afschuifvlakken kunnen worden genomen, maar dat vereist kennis uit de elasticiteitstheorie om evenredige verdelingen te kunnen garanderen. Daarom beperken we ons tot vlakke afschuifvlakken.

Fig. 28 Mogelijke gekromde afschuifvlakken, maar geen onderdeel van dit vak.

Geknikt afschuifvlakken zijn wel toegestaan, zolang elk vlakdeel maar loodrecht op de randen staat en voldoen aan de andere voorwaarden. Als een symmetrische doorsnede symmetrisch wordt doorgesneden, kunnen we uitgaan van een evenredig verdeelde schuifspanning op elk vlakdeel.

Fig. 29 Mogelijke geknikte afschuifvlak.

Ongeacht dat de richting van de schuifspanningen en daarmee de richting van het afschuifvlak niet altijd te bepalen zijn, kunnen we vanwege symmetrie op sommige delen van de doorsnede wel de richting bepalen (zonder waarde). In het middel van de getoonde doorsnedes moet de schuifspanning wel verticaal lopen, anders is er geen symmetrisch schuifspanningsverloop mogelijk.

Fig. 30 Richting van de schuifspanningen is bekend in het midden van de doorsnede vanwege symmetrie.

Voorbeeld

Het bepalen van de schuifspanningen voor een niet-rechthoekige doorsnede wordt getoond op onderstaande voorbeeld.

Voorbeeld

Fig. 31 Doorsnede en constructie

Gevraagd is de absolute waarde van schuifspanningen ergens in de doorsnede bij \(\rm{A}\).

Allereerst kunnen we de afschuifvlakken bepalen waar we de schuifspanningen kunnen berekenen. Deze afschuifvlakken moeten loodrecht op de randen worden genomen. Daarnaast mag het afschuifvlak niet genomen worden in de buurt van een overgang in breedte. Dat heeft tot gevolg dat de afschuifvlakken alleen in de getoonde delen kunnen worden genomen.

Fig. 32 Links afschuifvlakken die niet mogelijk zijn, rechts mogelijke afschuifvlakken.

We kunnen de schuifspanningen dus alleen bepalen in het diagonale gedeelte en dan niet te dicht bij de hoeken. We kiezen daarom voor een afschuifvlak op een vrij willekeurige hoogte van \(\bar{z} = -48 \, \rm{mm}\).

Fig. 33 Afschuifvlak gekozen op \(\bar{z} = -48 \, \rm{mm}\)

Nu moeten we eerst de doorsnedegrootheden worden bepaald, beginnend met het oppervlakte \(A\).

Fig. 34 Berekening oppervlakte

\[ A = 280 \cdot 140 \cdot \cfrac{1}{2} - 200 \cdot 100 \cfrac{1}{2} = 9600 \, \rm{mm^2} \]

Vervolgens kunnen we het zwaartepunt/normaalkrachtencentrum bepalen. Daarvoor verdelen we de constructie in parallellogrammen en driehoeken, elk met een eigen zwaartepunt.

Fig. 35 Onderverdeling van doorsnede in parallellogrammen en driehoeken voor het bepalen van het statisch moment, elk met een eigen zwaartepunt (\(\rm{C}\))

\[ \bar{z}_{\rm{N.C.}} = \cfrac{40 \cdot 100 \cdot 50 \cdot 2 + 80 \cdot 40 \cdot \cfrac{1}{2} \cdot \left(100 + \cfrac{1}{3} \cdot 40 \right)}{9600} = 60.\bar{5} \, \rm{mm} \]

Daarmee kan het traagheidsmoment \(I_{zz}\) worden bepaald, gebruik makend van dezelfde onderverdeling als voor het zwaartepunt.

\[\begin{split} \begin{align*} I_{zz} = & \,2 \cdot \left( \cfrac{1}{12} \cdot 40 \cdot 100^3 + 100 \cdot 40\ \cdot \left(60.\bar{5} - 50 \right)^2 \right) \\ & + \cfrac{1}{36} \cdot 80 \cdot 40^3 + 80 \cdot 40 \cdot \cfrac{1}{2} \cdot \left(60.\bar{5} - \left(100 + \cfrac{1}{3} \cdot 40 \right) \right)^2 \\ \approx & \, 12.2 \cdot 10^6 \, \rm{mm^4} \end{align*} \end{split}\]

Nu kan het statisch moment van het afschuivend deel worden bepaald. We kiezen voor een afschuifvlak met de hartlijn op \(\bar{z} = -48 \, \rm{mm}\). Het afschuivend deel nemen we het deel onder deze snede, hoewel we ook het andere deel hadden kunnen nemen, maar dat is complexer. Dit afschuivend deel is verdeeld in een gekantelde rechthoek en driehoek, waarvan de afmetingen volgen uit de goniometrie van de doorsnede.

Fig. 36 Afschuivend deel met afmetingen met N.C. van de hele doorsnede op \(60.\bar{5} \, \rm{mm}\) vanaf de onderkant en het snijpunt van snedevlak en hartlijn op \(-48 \, \rm{mm}\)

\[\begin{split} \begin{align*} S_{z}^{\rm{a}} = & \, 40 \cdot 20 \cdot \cfrac{1}{2} \cdot \left(60.\bar{5} - \cfrac{20}{3} \right)\\ & + 20 \sqrt{2} \cdot 38 \sqrt{2} \cdot \left(60.\bar{5} - \cfrac{38}{2} \right) \\ = & \, 84720 \, \rm{mm}^3 \\ \end{align*} \end{split}\]

Dit geeft:

\[ \tau = \cfrac{\left| V_z \, S_{z}^{\rm{a}} \right| }{I_{zz} \, t} \approx \cfrac{\left| 120000 \cdot 84720\right|}{12.2 \cdot 10^6 \cdot 20 \sqrt{2}} \approx 29.6 \, \rm{MPa} \]

Het resultaat is dus een evenredig verdeelde schuifspanning op ons schuifvlak. De werklijn is dwars op het afschuifvlak en evenwijdig aan de rand en de richting is nog niet bepaald. Het bepalen van de richting passen we pas een volgende keer toe bij dunwandige doorsneden.

Fig. 37 Afschuivend deel met afmetingen met N.C. van de hele doorsnede op \(60.\bar{5} \, \rm{mm}\) vanaf de onderkant en het snijpunt van snedevlak en hartlijn op \(-48 \, \rm{mm}\)

Alternatieve uitleg en voorbeeld

In voorbeeld 2 van hoofdstuk 5.4 van het boek Mechanica, spanningen, vervormingen en verplaatsingen (Hartsuijker and Welleman, 2016) komt een deel van de conclusies van dit hoofdstuk ook aan bod.

Oefeningen

Opgaves 5.7, 5.8, 5.29, 5.30, 5.32a-b in hoofdstuk 5 van het boek Mechanica, spanningen, vervormingen en verplaatsingen (Hartsuijker and Welleman, 2016). Antwoorden zijn hier beschikbaar.