Begeleide oefening 2

Gegeven is de volgende doorsnede:

Fig. 40 Voorbeelddoorsnede

Verder is gegeven dat voor een segment van een ring geldt:

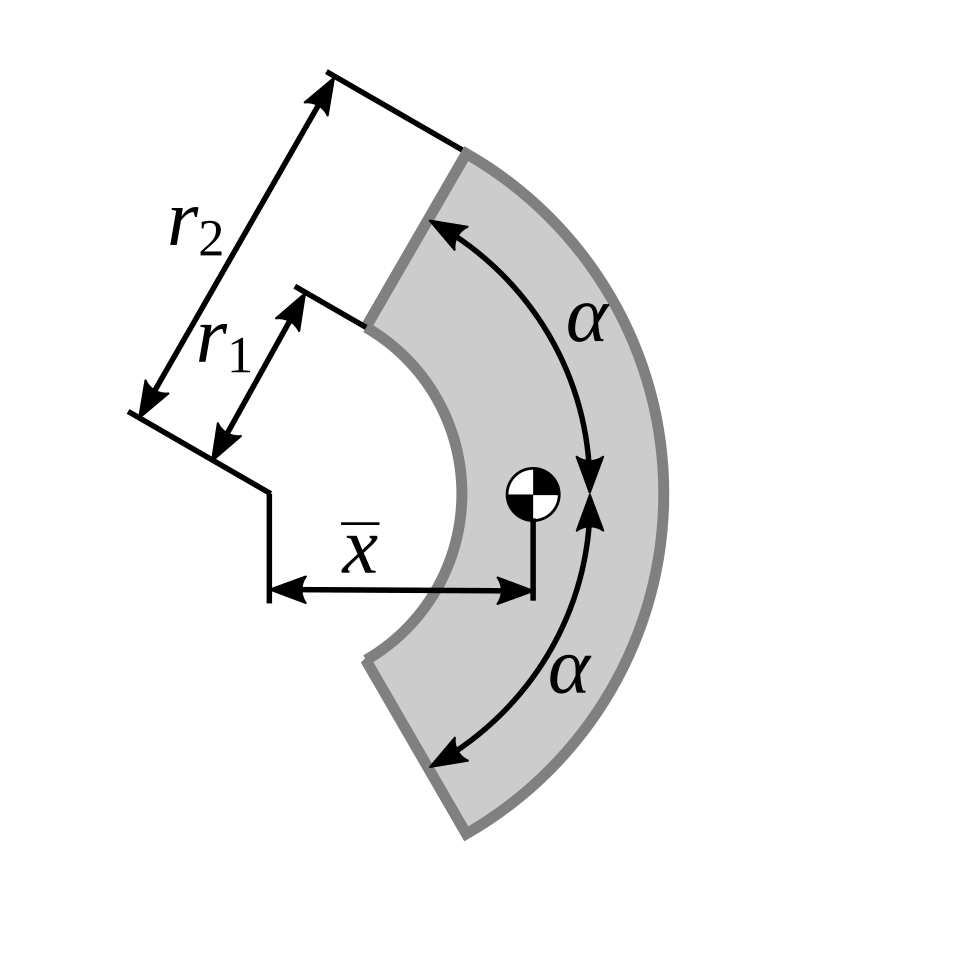
Fig. 41 Zwaartepunt \(\bar{x}\) van een ringsegment met binnenste straal \(r_1\), buitenste straal \(r_2\) en totale hoek \(2\alpha\).
Auteur: DuckRabbitDuckRabbit | Licentie: CC BY-SA 4.0 | Datum: 2020-12-13 | Auteursrecht: © DuckRabbitDuckRabbit 2020 | Bron: Wikimedia Commons

\[\begin{split} \begin{align*} A &= \alpha \left( r_2^2 - r_1^2 \right) \\ \bar{x} &= \cfrac{2 \sin \left( \alpha \right)}{ 3 \alpha} \cfrac{r_2^3 - r_1^3}{r_2^2 - r_1^2} \end{align*} \end{split}\]

Opgave

Gegeven zijn een aantal mogelijke punten waarop de schuifspanning kan worden bepaald:

Fig. 42 Doorsnede met mogelijke punten voor het bepalen van de schuifspanning.

Je mag er vanuit gaan dat \(R \gg b\) voor alle relevante afschuifvlakken.

Oplossing

…

Opgave

Gegeven zijn vier mogelijke schuifspanningsverdelingen.

Fig. 43 Vier mogelijke schuifspanningsverdelingen.

Oplossing

…

Opgave

Bepaal de doorsnedegrootheden

Oplossing

…

Opgave

Bepaal de maximale schuifspanning

Oplossing

…

Opgave

Waar is de schuifspanning de helft van de maximale waarde uitgedrukt als hoek van het afschuifvlak \(\varphi\) tov het assenstelsel tussen \(-\cfrac{\pi}{2}\) en \(0\) ten opzichte van de \(y\)-as.?

Fig. 44 Voorbeeld van een hoek

Oplossing

…