Exam Friday November 7th

Today you’ll make the first exam assignment covering Statically indeterminate structures including its prerequisites. For more information about the exam see the assessment information in course information

Exam assignment

Your own submission and its grading can be found here: exam assignment Statically indeterminate structures 1. The exam assignment was provided as follows:

Given is the structure as shown in the figure below.

Exercise

Show that this structure is statically indeterminate to the second degree.

Solution

For this structure, the external static indeterminacy is equal to the internal static indeterminacy.

There are 8 unknowns and 6 equilibrium equations, making the structure statically indeterminate to the second degree.

Exercise

Provide two alternative valid variants to make this structure statically determinate for the purpose of the force method or displacement method with statically indeterminate displacements. Provide two different variants: your adjustments must each modify a different part of the structure. For each of the variants, provide the necessary equation(s) to determine the statically indeterminate force(s) or statically indeterminate displacement(s).

Oplossing

Adding a hinge in the same segment or releasing a two-force-element in the same segment does not count as a valid variant.

A few potential variants are:

Veelgemaakte fouten

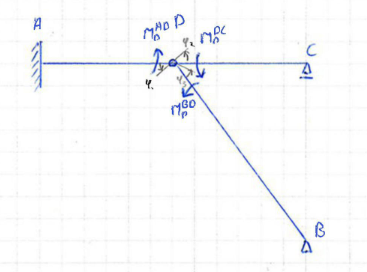
Fig. 186 Structure not statically determinate

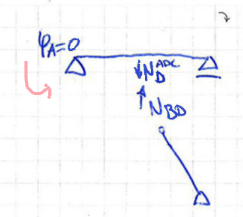
Fig. 187 Statically indeterminate force / displacement missing

Exercise

Determine the vertical support reaction in \(\rm{A}\) using the force-or displacement method

Oplossing

As an example, the force method has been applied using the following statically determinate system, but other methods are also acceptable:

The effect of temperature can be taken into account by a kinematically equivalent load on \(\rm{ADC}\):

\[ M^{\rm{T}} = 7875 \cdot 10^{-5} \cdot \cfrac{66.5}{0.25} = 20.9475 \ \rm{kNm}\]

This must be applied at both ends of \(\rm{ADC}\) to obtain a constant curvature.

The elongation of \(\rm{BD}\) can now be found using the elongation of a bar:

\[ \Delta L_{\rm{BD}} = \cfrac{N^{\rm{BD}} \cdot 5}{2000} = \cfrac{N^{\rm{BD}}}{400} = 0.0025 N^{\rm{BD}}\]

The displacement \(w_{\rm{D}}^{\rm{BD}}\) can now be found using Williot’s theorem:

\[ w_{\rm{D}}^{\rm{BD}} = -\cfrac{N^{\rm{BD}}}{400} \cdot \cfrac{5}{4} = -\cfrac{N^{\rm{BD}}}{320} = -0.003125 N^{\rm{BD}} \]

The displacement \(w_{\rm{D}}^{\rm{ADC}}\) and rotation \(\varphi_{\rm{A}}\) can now be found using the forget‑me‑nots:

\[\begin{split} \begin{align*} w_{\rm{D}}^{\rm{ADC}} &= \cfrac{M_{\rm{A}} \cdot 6^2}{16 \cdot 7875} - 2\cdot \cfrac{20.9475^2}{16 \cdot 7875} + \cfrac{N^{\rm{BD}} \cdot \cfrac{4}{5} \cdot 6^3}{48 \cdot 7875} \\ w_{\rm{D}}^{\rm{ADC}} &= \cfrac{M_{\rm{A}}}{3500} + \cfrac{2 \cdot N^{\rm{BD}}}{4375} - \cfrac{1197}{100000}\\ w_{\rm{D}}^{\rm{ADC}} &\approx 0.0002857 M_{\rm{A}} + 0.0004571 N^{\rm{BD}} - 0.01197 \\ \varphi_{\rm{A}} &= \cfrac{M_{\rm{A}} \cdot 6}{3 \cdot 7875} - \cfrac{20.9475 \cdot 6}{6 \cdot 7875} - \cfrac{20.9475 \cdot 6}{3 \cdot 7875} + \cfrac{N^{\rm{BD}} \cdot \cfrac{4}{5} \cdot 6^2}{16 \cdot 7875} \\ \varphi_{\rm{A}} &= \cfrac{M_{\rm{A}} \cdot 2}{7875} + \cfrac{N^{\rm{BD}}}{4375} - \cfrac{399}{50000}\\ \varphi_{\rm{A}} &\approx 0.000254 M_{\rm{A}} + 0.0002286 N^{\rm{BD}} - 0.00798 \end{align*} \end{split}\]

Solving for the displacement conditions gives:

\[\begin{split} \left\{ \begin{matrix} {w_{\rm{D}}^{\rm{ADC}}=w_{\rm{D}}^{\rm{BD}}} \\ {\varphi_{\rm{A}}=0} \end{matrix} \right. \;\to\; \begin{matrix} {M_{\rm{A}} = \cfrac{24489}{800} = 30.61125 \ \rm{kNm}} \\ {N_{\rm{BD}} = 0.9 \ \rm{kN}} \end{matrix} \end{split}\]

The vertical reaction in \(\rm{A}\) can now be determined using the equilibrium equations:

\[ \sum \left. T \right|_{\rm{C}}^{\rm{ADC}} = 0 \to A_{\rm{v}} = -\cfrac{7587}{1600} = -4.741875 \ \rm{kN} \left(\downarrow\right) \]

Veelgemaakte fouten

Fig. 188 Displacements due to forces in two-force member forgotten

Fig. 189 Rotation of two-force member not taken into account (Williot not used)

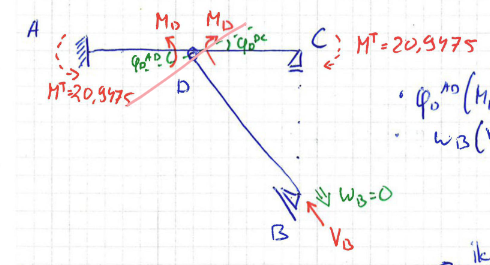
Fig. 190 Kinematically equivalent moment doesn’t give correct curvature

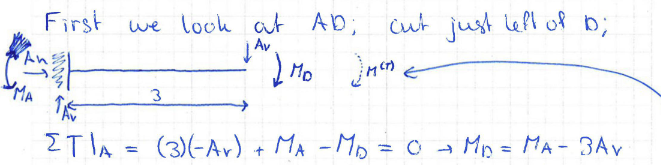
Fig. 191 Express forces and displacements in other unknowns than the statically indeterminate ones

Fig. 192 Solving just one equilibrium or compatibility equation