Lesson November 24th

Lesson November 24th#

During today’s lesson you’ll work on a complex exercise on the topic of the stress-strain relations. Please ask your questions regarding the homework as well!

Exercise stress-strain relations#

Given is the following stress element:

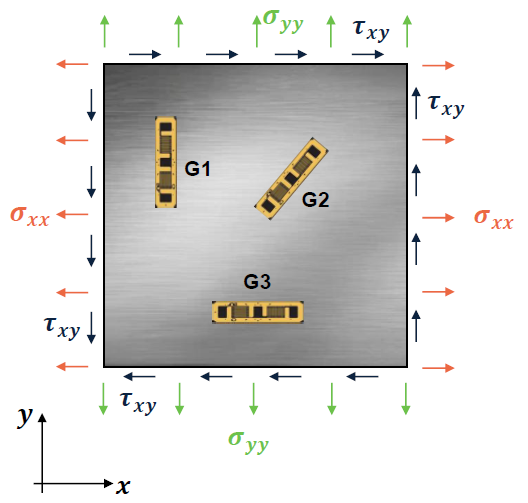
../../_images/image1.png

Fig. 195 Aluminium plate with strain gauges: \(E = 70 \ \rm{ GPa}\), \(\nu = 0.33 \ \rm{(-)}\), \(\varepsilon_{\rm{G1}} = -1.0 \cdot 10^{-3}\), \(\varepsilon_{\rm{G2}} = 2 \cdot 10^{-3}\), \(\varepsilon_{\rm{G3}} = +2 \cdot 10^{-3}\).#

  1. Find the strain tensor

  2. Find the principal strains

  3. Find the stress tensor

  4. Find the principal stresses

Solution assignment 1

\[\begin{split} \boldsymbol{\varepsilon} = \begin{bmatrix} 2 & 1.5 \\ 1.5 & -1 \end{bmatrix} \cdot 10^{-3} \end{split}\]

Solution assignment 2

  • \(\varepsilon_{1} = 2.62 \cdot 10^{-3}\)

  • \(\varepsilon_{2} = -1.62 \cdot 10^{-3}\)

Solution assignment 3

\[\begin{split} \begin{bmatrix} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \end{bmatrix} = \begin{bmatrix} 131.2 \\ -26.7 \\ 79.0 \end{bmatrix} \, \rm{ MPa} \end{split}\]

Solution assignment 4

  • \(\varepsilon_{1} = 163.9 \, \rm{MPa}\)

  • \(\varepsilon_{2} = -59.4 \, \rm{MPa}\)

Exercise stress-strain relations 2#

Given is the following stress element:

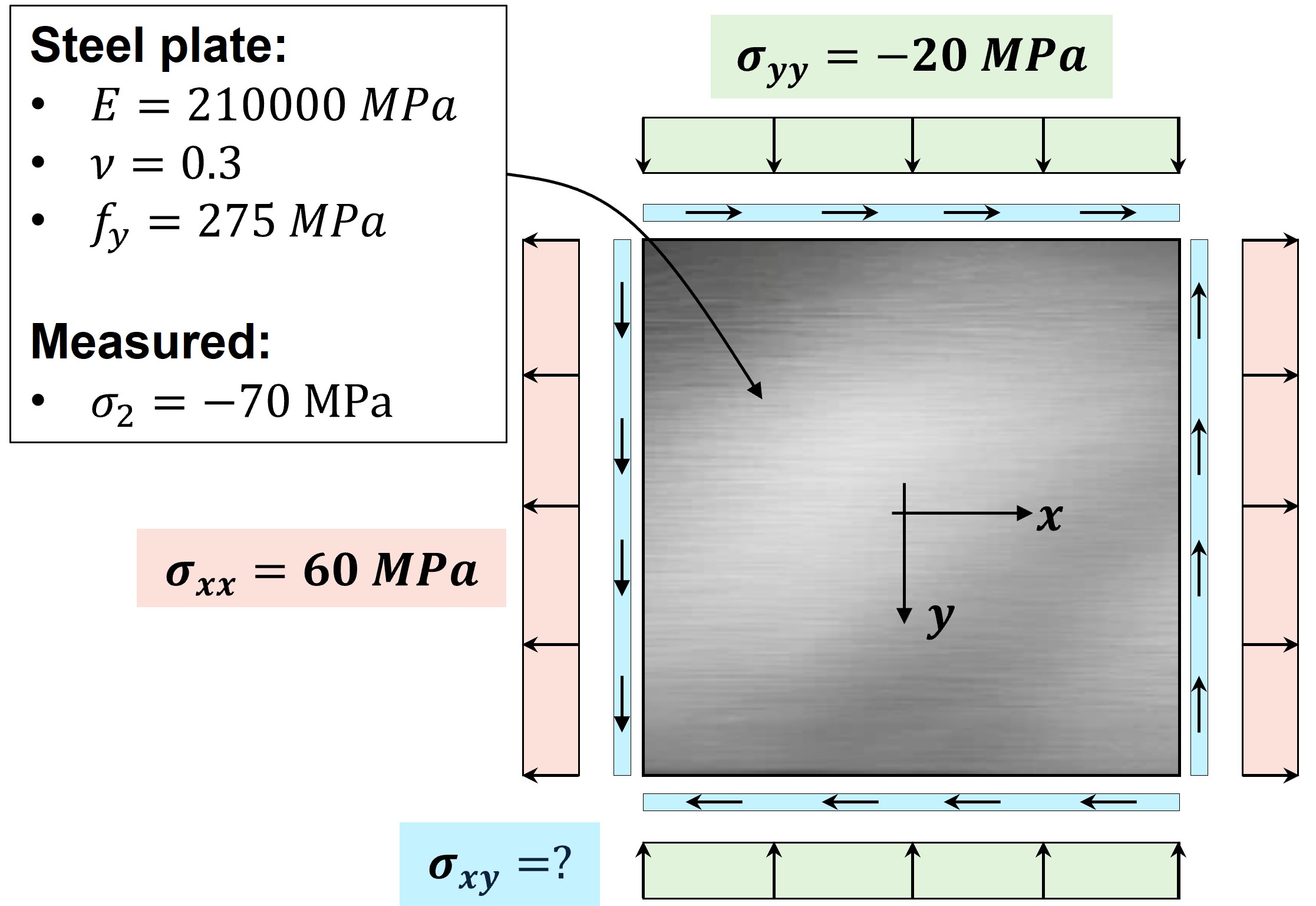
../../_images/Figure_exam_general.jpg

Fig. 196 This plate of steel (\( E =210000 \, \rm{MPa}, \nu = 0.3, f_y =275 \, \rm{MPa}\)) is tested in homogeneous plane stress conditions. It is measured that \( \sigma_{xx} = 60 \, \rm{MPa}\) and \(\sigma_{yy} = -20 \, \rm{ MPa}\). (Note: in the drawing, the normal stress in y-direction is already represented in compression) We also know that the value of the minimum principal stress is \(\sigma_2=−70 \, \rm{ MPa}\)#

  1. Compute the value of the shear stress \(\sigma_{xy}\) (assume a positive value for \(\sigma_{xy}\)).

  2. Compute \(\varepsilon_{xx}\), \(\varepsilon_{yy}\), \(\varepsilon_{xy}\) and \(\varepsilon_{zz}\).

Solution assignment 1

\[ \sigma_{xy} \approx 80.62 \, \rm{MPa}\]

Solution assignment 2

  • \(\varepsilon_{xx} = 0.000314\)

  • \(\varepsilon_{yy} = -0.000181\)

  • \(\varepsilon_{xy} = 0.000499\)

  • \(\varepsilon_{zz} = -0.000057\)

Contents