Lesson November 21th

Lesson November 21th#

During today’s lesson you’ll work on a complex exercise on the topic of the Transforming tensors. Please ask your questions regarding the homework as well!

Exercise Transforming tensors#

Given is the following structure and cross-section:

../../_images/structure6.svg

  1. Find the relevant cross-sectional properties.

  2. Find the normal and shear stresses just below \(\rm{G}\), in \(\rm{H}\), in \(\rm{I}\) and just right of \(\rm{C}\) in cross-section \(\rm{A}\).

  3. Find the principal values of the stresses in the points just below \(\rm{G}\), in \(\rm{H}\), in \(\rm{I}\) and just right of \(\rm{C}\) in cross-section \(\rm{A}\).

Solution assignment 1

Normal force centre is given by:

../../_images/NC2.svg

  • \(A \approx 17500 \,\rm{ mm}^2\)

  • \(I_{zz} \approx 655 \cdot 10^6 \, \rm{ mm}^4\)

Solution assignment 2

  • \(\sigma_{\rm{just} \,\rm{below} \,\rm{G}} = +6.73 \,\rm{ MPa}\)

  • \(\tau_{\rm{just} \,\rm{below} \,\rm{G}} = +0.164 \,\rm{ MPa}\)

  • \(\sigma_{\rm{H}} = +6.73 \,\rm{ MPa}\)

  • \(\tau_{\rm{H}} = 0 \,\rm{ MPa}\)

  • \(\sigma_{\rm{I}} = -2 \,\rm{ MPa}\)

  • \(\tau_{\rm{I}} = +0.35 \,\rm{ MPa}\)

  • \(\sigma_{\rm{just} \,\rm{right} \,\rm{of} \,\rm{C}} = -8.53 \,\rm{ MPa}\)

  • \(\tau_{\rm{just} \,\rm{right} \,\rm{of} \,\rm{C}} = -0.12 \,\rm{ MPa}\)

Solution assignment 3

  • \(\sigma_{\rm{1,} \,\rm{just} \,\rm{below} \,\rm{G}} = +6.73 \,\rm{ MPa}\)

  • \(\sigma_{\rm{2,} \,\rm{just} \,\rm{below} \,\rm{G}} = -0.0040 \,\rm{ MPa}\)

  • \(\sigma_{\rm{1,} \,\rm{H}} = +6.73 \,\rm{ MPa}\)

  • \(\sigma_{\rm{2,} \,\rm{H}} = 0 \,\rm{ MPa}\)

  • \(\sigma_{\rm{1,} \,\rm{I}} = 0.059 \,\rm{ MPa}\)

  • \(\sigma_{\rm{2,} \,\rm{I}} = -2.06 \,\rm{ MPa}\)

  • \(\sigma_{\rm{1,} \,\rm{just} \,\rm{right} \,\rm{of} \,\rm{C}} = 0.0018 \,\rm{ MPa}\)

  • \(\sigma_{\rm{2,} \,\rm{just} \,\rm{right} \,\rm{of} \,\rm{C}} = -8.5 \,\rm{ MPa}\)

Exercise stress tensor#

Given is the following structure and cross-section:

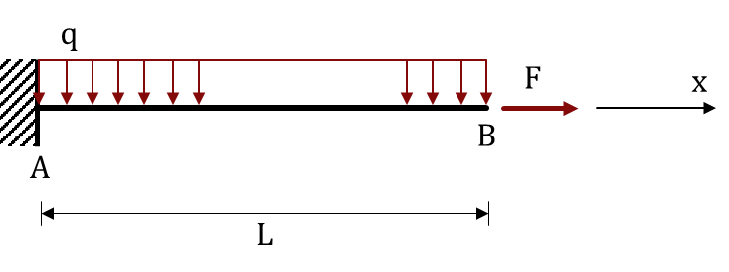
../../_images/constructie.png

Fig. 193 Structure, with properties \(L = 4 \,\rm{ }\), \(F = 200 \,\rm{ kN}\), \(q = 20 \,\rm{ kN/m}\)#

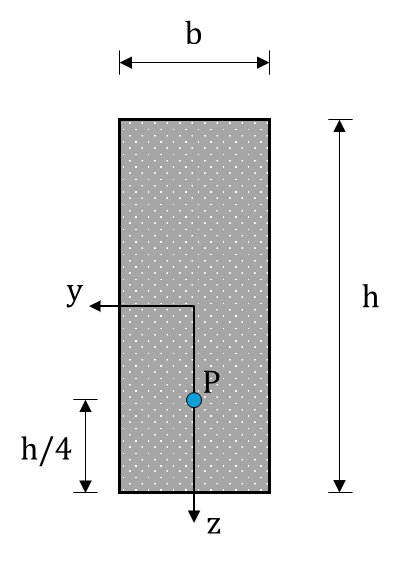
../../_images/doorsnede.png

Fig. 194 Cross-section, with properties: \(E = 30 \,\rm{ GPa}\), \(\nu = 0.2 \,\rm{(-)}\), \(b = 200 \,\rm{ mm}\), \(h = 600 \,\rm{ mm}\).#

  1. Find the internal forces in cross-section \(\rm{A}\).

  2. Find the stresses in point \(\rm{P}\) in cross-section \(\rm{A}\).

  3. Find the stress tensor in the \(xyz\)-coordinates in point \(\rm{P}\) in cross-section \(\rm{A}\).

  4. Find the isotropic and deviatoric components.

Solution assignment 1

  • \(N_{\rm{A}} = 200 \, \rm{ kN}\)

  • \(V_{\rm{A}} = 80 \, \rm{ kN}\)

  • \(M_{\rm{A}} = -160 \, \rm{ kNm}\)

Solution assignment 2

  • \(\sigma_{yy} = \sigma_{xy} = \sigma_{yz} = \sigma_{zz} = 0 \, \rm{ MPa}\)

  • \(\sigma_{xx} = -5 \, \rm{ MPa}\)

  • \(\sigma_{xz} = 0.75 \, \rm{ MPa}\)

Solution assignment 3

\[\begin{split} \boldsymbol{\sigma} = \begin{bmatrix} -5 & 0 & 0.75 \\ 0 & 0 & 0 \\ 0.75 & 0 & 0 \end{bmatrix} \, \rm{ MPa} \end{split}\]

Solution assignment 4

\[\begin{split} \boldsymbol{\sigma} = \begin{bmatrix} -1.67 & 0 & 0 \\ 0 & -1.67 & 0 \\ 0 & 0 & -1.67 \end{bmatrix} + \begin{bmatrix} -3.33 & 0 & 0.75 \\ 0 & 1.67 & 0 \\ 0.75 & 0 & 1.67 \end{bmatrix} \, \rm{ MPa} \end{split}\]
Contents