Begeleide oefening 3#
Gegeven is de volgende constructie:
Fig. 50 Constructie#
Bepaal de oplegreacties, verplaatsingen en het krachtsverloop in de constructie met MatrixFrame.
Opgave
Voer de geometrie in en ga verder met de profielgegevens.
Oplossing
Vraag 1:
\(EI = 0\)
Onjuist, MatrixFrame heeft een waarde ongelijk aan 0 nodig om de constructie door te kunnen rekenen. Heeft de waarde van EI invloed op je antwoord?
Een willekeurige maar kleine waarde
Onjuist, aangezien er geen kracht staat op de kabels, kan deze ook als pendelstaaf worden gemodelleerd? wat is de invloed van EI op het vervormingsgedrag van de kabels?
Een willekeurige waarde
Exact, waarom maakt het voor de kabels niet uit wat de waarde is van EI? Waarom kunnen deze als pendelstaven worden gemodelleerd?
Vraag 2:
\(EI = \infty\)
Onjuist, een waarde van oneindig kan je niet invullen. Hoe kan je dat numeriek benaderen?
Een willekeurige, maar grote, waarde
Correct, welke waarde kies je?
Een willekeurige waarde
Onjuist, als je een kleine stijfheid invoert zal dat zeker geen oneindige waarde simuleren.
Opgave
Ga verder met opleggingen.
Oplossing
Een pendelstaaf dwars op de rolrichting van het rolscharnier toevoegen
Correct, wat voor profielgegevens voeg je toe voor deze pendelstaaf?
Roloplegging in zowel horizontale als verticale oplegging toevoegen
Onjuist, dan heb je er een reguliere scharnierende verbinding van gemaakt
Er is geen alternatief
Onjuist, een pendelstaaf staat bij kleine verplaatsingen ook in één richting beweging toe.
Opgave
Voer de scharnierende aansluitingen in, voer de linear-elastische berekening uit en bekijk de resultaten.
Oplossing
De maximale verplaatsing van BC in verticale richting is 0.27 m
De maximale zakking van AD in verticale richting is 1.42 cm
De grootste normaalkracht in de kabels is 303.08 kN
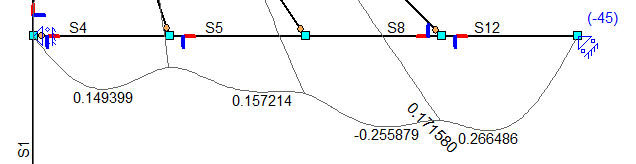
Fig. 51 Maximale verplaatsing van BC#
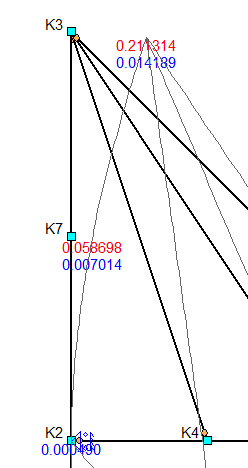
Fig. 52 Maximale zakking van AD#
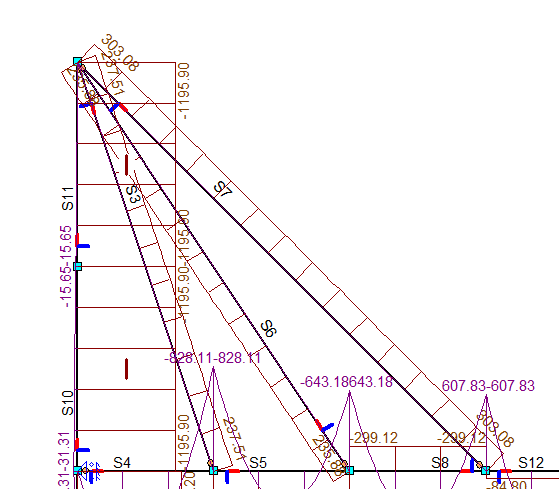
Fig. 53 Maximale zakking van AD#
Hint
Het bestand van dit voorbeeld is hier te downloaden.
